Website

Welcome!

This is a place chosen to make available some ideas (on puzzles, patterns, etc)

that seemed unsuitable for posting in a Forum, but some people may find interesting.

For difficult puzzles (like the next one), possible solutions will not be shown (only hints).

For other puzzles, the solution wil be hidden so that a serious attempt can be made

without direct access to a solution.

(hopefully this will make the puzzles more interesting for newcomers).

Puzzles

Puzzle #1 (Classic 9x9 Sudoku (SER = 8.4); Proposed Feb 12, 2024)

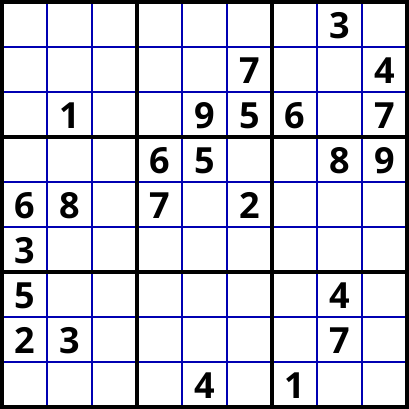
The following Classic Sudoku Puzzle (SER = 8.4) was generated in April, 2021

using HoDoKu for a training practice with als/ahs.

I solved it (manually) in two main steps

(i.e., apart from moves with scope in a single house - the "basics").

SER = 8.4

(image created using SudokuExplainer)

After performing the basics, find non-basic moves that solve this puzzle.

Hint

After performing all basic eliminations, write all condidates

.--------------------------------------------------------------.
| 126    1269   5     | 4     79   3   | 8      179     1279   |
| 123    8      234   | 159   579  6   | 12479  134579  123579 |
| 7      1349   34    | 1589  2    58  | 6      13459   1359   |
|---------------------+----------------+-----------------------|
| 28     24     1     | 59    48   7   | 3      6       59     |
| 68     5      678   | 3     89   1   | 79     2       4      |
| 9      347    347   | 6     45   2   | 17     157     8      |
|---------------------+----------------+-----------------------|
| 13568  1367   9     | 2     36   458 | 147    13478   137    |
| 2358   237    2378  | 578   1    458 | 2479   34789   6      |
| 4      12367  23678 | 78    36   9   | 5      1378    1237   |
'--------------------------------------------------------------'

and

(a) look at the pattern of 2s to get some eliminations,

(b) Now, study carefully boxes 1 (top-left) and 4 (middle-left).

A very strong Sudoku player found a great solution in one step.

(items (a),(b) are for a solution in two steps)

Puzzle #2 (9x9 Jigsaw Sudoku Puzzle (SER=8.0); Proposed Feb 18, 2024)

The following Jigsaw Sudoku Puzzle was generated in Feb, 2024

using 1to9only new release of SudokuExplainer.

The puzzle is rated SER = 8.0, and it can be solved (manually) in

four main steps.

SER = 8.0

(image created using SudokuExplainer)

Hint

After basics (and having listed all candidates in each cell), find an UR, then an X-chain, and two wings.

Puzzle #3 (5x5 Latin Squares Puzzle (SER = 8.3); Proposed Feb 21, 2024)

The following 5x5 Latin Squares Puzzle (generated with SudokuExplainer)

is rated SER = 8.3, and can be solved (manually) in four main steps.

SER = 8.3

(image created using SudokuExplainer)

Hint

(columns counted from left to right and rows from top to bottom)

First write all candidates in each cell.

Step 1: We can eliminate 3 from r2c4 using a sequence of bivalued cells.

Step 2: the harder part! (the reason for that SE rating).

The suggestion is to study carefully the grid and try to find a way

to show that 2 is false at that same cell r2c4.

If Step 2 is done, the puzzle can be solved in two more moves.

For the last move, there is a pretty, simple idea!

Puzzle #4 (proposed Mar 8, 2024)

Write a detailed solution to the following interesting 6x6 Slitherlink puzzle:

(From Simon Tatham's Portable Puzzle Collection)

6x6 hard Slitherlink puzzle

Hint

This puzzle (rated hard) can be solved (manually) in 12 steps using well-known patterns.

The start (4 steps) uses well-known patterns. Other two patterns are proposed as Problems.

The idea of writing out a detailed solution path is to break the solution into n parts

where each part is a well-identified pattern (some are shown in Problems below) that can be

used in other puzzles (and hopefully has a short and elegant proof).

Puzzle #5 (proposed Mar 11, 2024)

Write a detailed solution to the following hard 5x5 Hidoku puzzle:

5x5 Hidato puzzle (hard)

(Found recently by Albert.Lang)

I found an interesting reasonably simple and short (manual) solution to this puzzle

and for this reason I decided to propose it here.

(the restrictive rule of including the first and last digits in the givens is waived)

Remark

This pattern has the smallest number of clues for a 5x5 Hidoku with unique solution.

I'd be interested to know of other ways, essentially different from this one.

Puzzle #6 (proposed Mar 31, 2024)

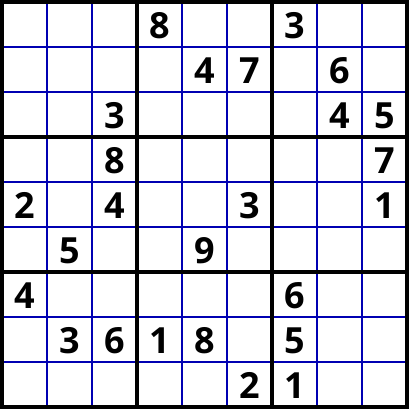
After basics, find a move that solves this Classic Sudoku puzzle ("three waves", SER = 7.2):

Classic Sudoku (SER = 7.2)

(image created using SudokuExplainer)

This puzzle was found with Sudoku Architect when I was playing around with waves.

Hint

Look for a fish !

Puzzle #7 (proposed April 20, 2024)

After basics, this Classic Sudoku puzzle (SER = 8.3) can be solved in just two non-basic steps:

Classic Sudoku (SER = 8.3)

(image created using SudokuExplainer)

This puzzle was found in the same way as #6.

Hint

There also an unique one-stepper.

Problems

Problem #1

In the game called Slitherlink, show all the details

proving that the following configuration is impossible

Impossible pattern 222x

Hidden solution

Part 1

(My solution has a trivial initial observation, an easy Case 1 and Case 2 divided in two sub-cases)

We analyze the possible outcomes from this configuration but can already discard

all configurations in which the lower "2"-cell has vertical lines, or horizontal lines,

in both edges.

Also, this configuration

.-------------------
| .   .   .   .   . 
|           2       
| .   .   .   .   . 
|       2           
| .___.   .   .   . 
| | 2               
|A.   .   .   .   . 
| x                 
| .   .   .   .   .

and this

.-------------------
| .   .   .   .   . 
|           2       
| .   .   .   .   . 
|       2           
| .   .   .   .   . 
|   2 |             
|A.___.   .   .   . 
| x                 
| .   .   .   .   .

are clearly impossible,

(dead end at corner A).

Part 2

Case 1:

.-------------------
| .   .   .   .   . 
|           2       
| .   .   .   .   . 
|       2           
| .___.   .   .   . 
|   2 |             
| .   .   .   .   . 
| x                 
| .   .   .   .   .

Now the following is forced

.-------------------
| .   .___.___.   . 
|         x 2 |     
| .   .___. x .   . 
| |   x 2 |         
| .___. x .   .   . 
|   2 |             
| .   .   .   .   . 
| x                 
| .   .   .   .   .

and this leads to an impossibility in the cell at the corner, reached by three lines.

Part 3

Case 2:

.-------------------
| .   .   .   .   . 
|           2       
| .   .   .   .   . 
|       2           
| .   .   .   .   . 
| | 2               
| .___.   .   .   . 
| x                 
| .   .   .   .   .

The following is a forced move

.-------------------
| .   .   .   .   . 
|           2       
| .   .B  .   .   . 
| |     2           
| . x .A  .   .   . 
| | 2 x             
| .___.   .   .   . 
| x                 
| .   .   .   .   .

Part 3.1

Case 2.1: If a vertical line exists at AB, it forces

.-------------------
| .   .   .   .   . 
|     |     2       
| .C  .   .   .   . 
| |   | 2           
| . x .___.D  .   . 
| | 2 x             
| .___.   .   .   . 
| x                 
| .   .   .   .   .

and any continuation for the line meeting corner C will create a loop (impossible).

Part 3.2

Case 2.2: the other possibility is to have the edge AB blocked, and then the bottom edge AD

of the "2"-cell in the middle needs to be blocked too, forcing the following configuration to be reached.

.-------------------
| .   .___.___.   . 
|         x 2 |     
| .   .___. x .   . 
| |   x 2 |         
| . x . x .   .   . 
| | 2 x             
| .___.   .   .   . 
| x                 
| .   .   .   .   .

Now, we have an impossible situation in the cell at the corner, reached by three lines. □

(Using symmetry, the proven result establishes a well-known slitherlink pattern)