
Welcome!
This is part of JCOWebsite and contains the proposed...
Write a detailed solution to the following hard Hidoku puzzle:
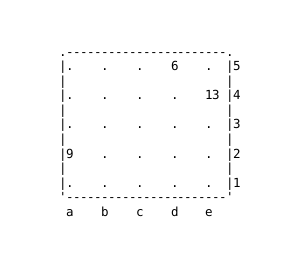
(Found by Albert.Lang)
I found an interesting reasonably simple and short (manual) solution to this puzzle
and for this reason I decided to propose it here.
(the restrictive rule of including the first and last digits in the givens is waived)
This pattern has the smallest number of clues for a 5x5 Hidoku with unique solution.
.-----------------------. |. . . 6 . |5 | | |. . *7 . 13 |4 | | |. *8 x . . |3 | | |9 . . . . |2 | | |. . . . . |1 '-----------------------' a b c d e
After the forced start, the possible values for x are very limited. For instance, for x=11, we must have
a1=25,b1=24 and the connection of 13 to 24 demands 10 cells, but placing 12 will destroy any possible way.
I propose the following Hidoku puzzle (my first Hidoku puzzle).
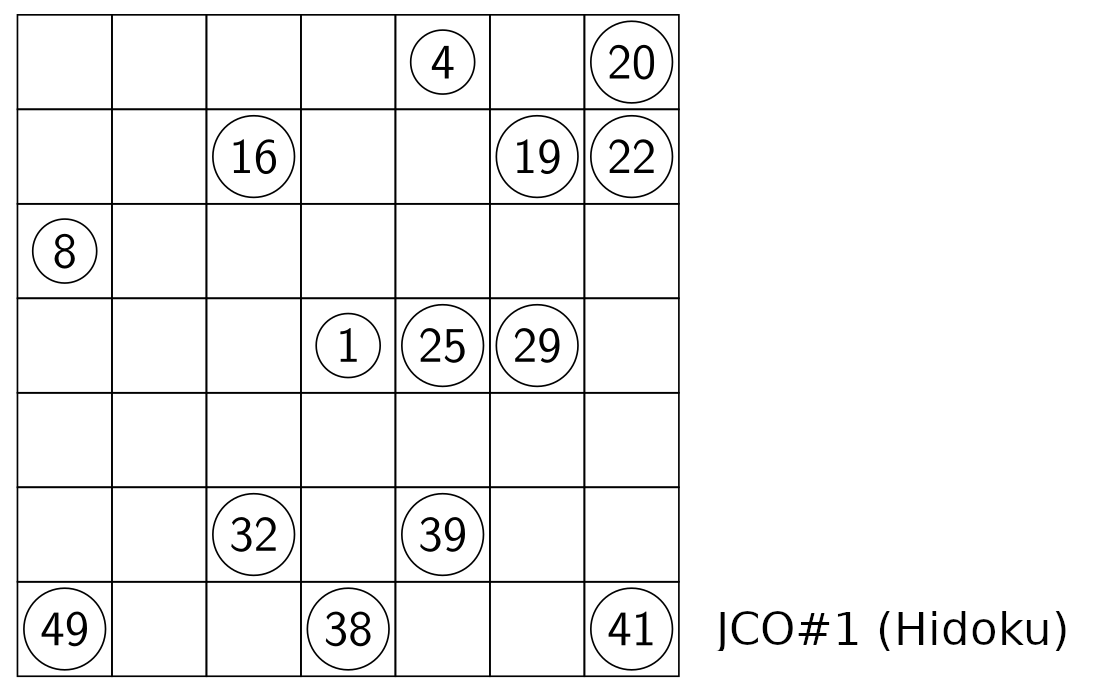
Fill the grid so that consecutive numbers must be neighbours horizontally, vertically, or diagonally.
Update 1 (Jul 12, 2025)
Remark: the initial grid below is correct.
,----------------------------,
| __ __ __ __ _4 __ 20 |7
| __ __ 16 __ __ 19 22 |6
| _8 __ __ __ __ __ __ |5
| __ __ __ _1 25 29 __ |4
| __ __ __ __ __ __ __ |3
| __ __ 32 __ 39 __ __ |2
| 49 __ __ 38 __ __ 41 |1
'----------------------------'
a b c d e f g JCO#1 (7x7 Hidoku)
The previous version of the edited image (.png) of the puzzle had two errors:
(16)b6 instead of the correct (16)c6, and (8)a5 was missing.
So, the image of the puzzle and the hint below only makes sense as of today (July 12).
I enjoyed greatly the task of creating this puzzle. For those willing to solve it
without guessing and willing to justify carefully each step, this is a tough puzzle.
There are two easy numbers at the start:
1.(21)f7 2.(30)e3
,----------------------------,
| __ __ __ __ 04 *21 20 |7
| __ __ 16 __ __ 19 22 |6
| 08 __ __ __ __ __ __ |5
| __ __ __ 01 25 29 __ |4
| __ __ __ __ *30 __ __ |3
| __ __ 32 __ 39 __ __ |2
| 49 __ __ 38 __ __ 41 |1
'----------------------------'
a b c d e f g JCO#1 (7x7 Hidoku)
(numbers with * are deduced and numbers without * were given)
We cannot link (4)e7 to (8)a5 using the route (5)d6-(4)c5. Why ?
This observation gives six more placements.
Update 2 (Jul 13, 2025)
After the moves
3.(6)c7! 4.(7)b6 5.(15)b7! 6.(14)a7 7.(13)a6 8.(12)b5
we reach the grid
,----------------------------,
|*14 *15 *06 __ 04 *21 20 |7
|*13 *07 16 __ __ 19 22 |6
| 08 *12 __ __ __ __ __ |5
| __ __ __ 01 25 29 __ |4
| __ __ __ __ *30 __ __ |3
| __ __ 32 __ 39 __ __ |2
| 49 __ __ 38 __ __ 41 |1
'----------------------------'
a b c d e f g JCO#1 (7x7 Hidoku)
(! means that a small deduction is involved)
How to proceed ?
Update (Jul 14, 2025)
We reached the first key configuration for this puzzle. Now,
. The route from (16)c6 to (19)f6 cannot go through d7/d6,e6 (Why ?)
. We cannot have both (17)d5, (18)e5 (why ?)
. (17)d6 and (18)d7 lead to an empty cell! (how ?)
Using these observations we arrive at
9.(17)d5!! 10.(18)d6! 11.(3)d6! 12.(5)d7 13.(31)d3! 14.(26)f3!
[!! means that the move is justified by more involved deduction]
We reach this configuration
,----------------------------,
|*14 *15 *_6 *_5 _4 *21 20 |7
|*13 *_7 16 *_3 *18 19 22 |6
| _8 *12 __ *17 __ __ __ |5
| __ __ __ _1 25 29 __ |4
| __ __ __ *31 *30 *26 __ |3
| __ __ 32 __ 39 __ __ |2
| 49 __ __ 38 __ __ 41 |1
'----------------------------'
a b c d e f g JCO#1 (7x7 Hidoku)
How to proceed ?
Update (July 16, 2025)
Now, to connect (49)a1 to (41)g1 we cannot take the path
that includes c1-d2-e1 (why ?). So,
15.(37)c1!
,----------------------------,
|*14 *15 *_6 *_5 _4 *21 20 |7
|*13 *_7 16 *_3 *18 19 22 |6
| _8 *12 __ *17 __ __ __ |5
| __ __ __ _1 25 29 __ |4
| __ __ __ *31 *30 *26 __ |3
| __ __ 32 __ 39 __ __ |2
| 49 __ *37 38 __ __ 41 |1
'----------------------------'
a b c d e f g JCO#1 (7x7 Hidoku)
How to proceed ? This is the second key situation in this puzzle.
A careful analysis of the left-side [EDIT (Jul 20): correct is right-side]
of the puzzle will produce the final deduction that solves the puzzle
with simple moves afterwards.
Update (Jul 20, 2025) The only two possible places for number 2 and the narrow passage at e1,d2,c3 can be used to solve this puzzle. The starting point is to study the consequences of (2)e5. This has an immediate effect on the right side that propagates through that narrow passage into certain q numbers being locked into q cells, leading to a contradiction. So, 16.(2)c5!! breaks the last resistance at solving this puzzle with easy placements. Btw, as always, I may be missing a much simpler way to solve the puzzle. This is the risk one must accept when decides to solve puzzles manually. To conclude: this puzzle involves reasonings with conflicting paths, narrow passages and locked sets (term borrowed from sudoku). 14 15 6 5 4 21 20 13 7 16 3 18 19 22 8 12 2 17 24 23 28 9 10 11 1 25 29 27 34 33 47 31 30 26 43 35 48 32 46 39 44 42 49 36 37 38 45 40 41
I propose the following Hidoku puzzle (my second Hidoku puzzle).
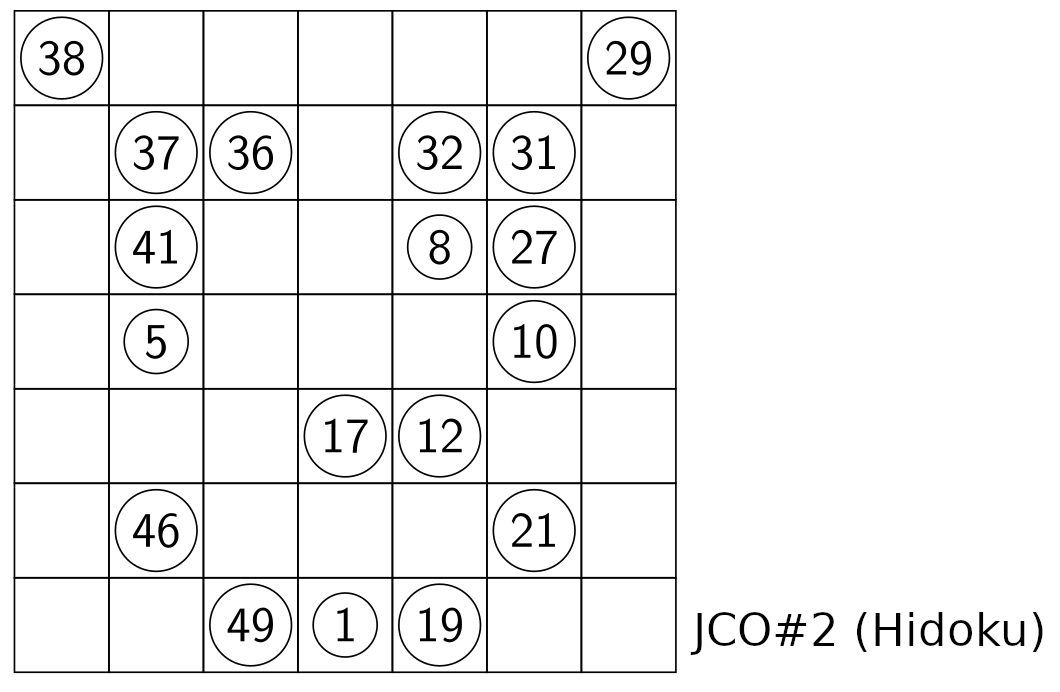
Update 1 (July 12, 2025)
This second puzzle is certainly easier than the first. One can get
many numbers making small deductions (like the basics in sudoku).
For reference, the initial grid is
,----------------------------,
| 38 __ __ __ __ __ 29 |7
| __ 37 36 __ 32 31 __ |6
| __ 41 __ __ 8 27 __ |5
| __ 5 __ __ __ 10 __ |4
| __ __ __ 17 12 __ __ |3
| __ 46 __ __ __ 21 __ |2
| __ __ 49 1 19 __ __ |1
'----------------------------'
a b c d e f g JCO#2 (7x7 Hidoku)
The basics in my solving has 16 moves.
The four first moves are 1.(9)e4 2.(11)f3 3.(28)g6 4.(30)f7
Update (Jul 13/14, 2025)
After the moves
1.(9)e4 2.(11)f3 3.(28)g6 4.(30)f7 5.(26)g5!
6.(25)g4 7.(24)g3 8.(23)g2 9.(22)g1 10.(39)b7!
11.(40)a6 12.(20)f1! 13.(18)e2 14.(33)e7!
15.(34)d7 16.(35)c7
we reach the configuration
,----------------------------,
| 38 *39 *35 *34 *33 *30 29 |7
|*40 37 36 __ 32 31 *28 |6
| __ 41 __ __ 8 27 *26 |5
| __ 5 __ __ *9 10 *25 |4
| __ __ __ 17 12 *11 *24 |3
| __ 46 __ __ *18 21 *23 |2
| __ __ 49 1 19 *20 *22 |1
'----------------------------'
a b c d e f g JCO#2 (7x7 Hidoku)
How to proceed ?
Update (Jul 18, 2025)
This position is interesting. We have two possibilities for 13.
In the case of (13)d2, we get a sequence of forced moves resulting
in 6,7,15,16 locked at the cells c4,c5,d4,d5,d6 and either 42 xor
4 must be there. But in either case we arrive at a disconnection
between consecutive numbers. So,
17.(13)d4!! and the remaining moves are easy.
38 39 35 34 33 30 29
40 37 36 7 32 31 28
42 41 6 14 8 27 26
43 5 15 13 9 10 25
44 4 16 17 12 11 24
45 46 3 2 18 21 23
47 48 49 1 19 20 22
I propose the following Hidoku puzzle (my third Hidoku puzzle).
This is the last Hidoku puzzle (for now), being roughly at the same level as #60.
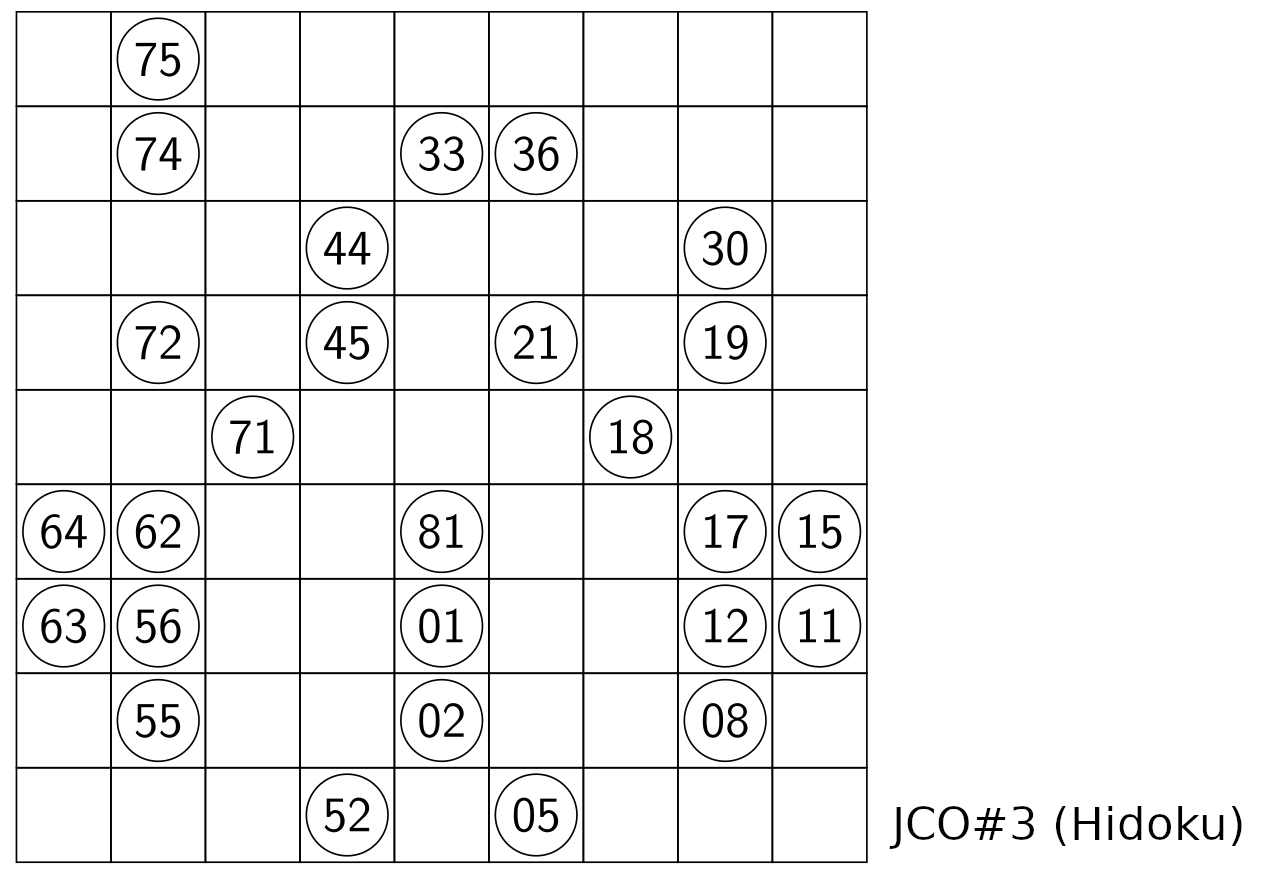
Grid with Givens
,----------------------------------,
|__ 75 __ __ __ __ __ __ __| 9
|__ 74 __ __ 33 36 __ __ __| 8
|__ __ __ 44 __ __ __ 30 __| 7
|__ 72 __ 45 __ 21 __ 19 __| 6
|__ __ 71 __ __ __ 18 __ __| 5
|64 62 __ __ 81 __ __ 17 15| 4
|63 56 __ __ 01 __ __ 12 11| 3
|__ 55 __ __ 02 __ __ 08 __| 2
|__ __ __ 52 __ 05 __ __ __| 1
'----------------------------------'
a b c d e f g h i JCO#3 (Hidoku)
(Jul 15, 2025 - revised Jul 28, 2025)
EDIT: I revised the whole solution. The initial
move 1. (20)g6 of the previous version was found
a lot later [paper and pencil solution].
The first moves are (indicated with * in the grid):
1.(80)d5 2.(79)c6 3.(78)b7 4.(77)a8 5.(76)a9
5.(14)h5 7.(13)g4 8.(10)i2 9.(9)i1 10.(7)h1
11.(16)i5 12.(29)i6 13.(28)i7
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
| __ *78 __ 44 __ __ __ 30 *28| 7
| __ 72 *79 45 __ 21 __ 19 *29| 6
| __ __ 71 *80 __ __ 18 *14 *16| 5
| 64 62 __ __ 81 __ *13 17 15| 4
| 63 56 __ __ 01 __ __ 12 11| 3
| __ 55 __ __ 02 __ __ 08 *10| 2
| __ __ __ 52 __ 05 __ *07 *09| 1
'-----------------------------------'
a b c d e f g h i
How to proceed ?
Update (Jul 18, 2025 - revised Jul 28, 2025)
14.(73)a7! (why ?)
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
|*73 *78 __ 44 __ __ __ 30 *28| 7
| __ 72 *79 45 __ 21 __ 19 *29| 6
| __ __ 71 *80 __ __ 18 *14 *16| 5
| 64 62 __ __ 81 __ *13 17 15| 4
| 63 56 __ __ 01 __ __ 12 11| 3
| __ 55 __ __ 02 __ __ 08 *10| 2
| __ __ __ 52 __ 05 __ *07 *09| 1
'-----------------------------------'
a b c d e f g h i
What would be a good next move ?
Update (Jul 21, 2025 - revised Jul 28, 2025)
15.(65)a5! 16.(66)a6 17.(67)b5 18.(68)c4
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
|*73 *78 __ 44 __ __ __ 30 *28| 7
|*66 72 *79 45 __ 21 __ 19 *29| 6
|*65 *67 71 *80 __ __ 18 *14 *16| 5
| 64 62 *68 __ 81 __ *13 17 15| 4
| 63 56 __ __ 01 __ __ 12 11| 3
| __ 55 __ __ 02 __ __ 08 *10| 2
| __ __ __ 52 __ 05 __ *07 *09| 1
'-----------------------------------'
a b c d e f g h i
19.(70)d4 20.(61)c3 21.(69)d3
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
|*73 *78 __ 44 __ __ __ 30 *28| 7
|*66 72 *79 45 __ 21 __ 19 *29| 6
|*65 *67 71 *80 __ __ 18 *14 *16| 5
| 64 62 *68 *70 81 __ *13 17 15| 4
| 63 56 *61 *69 01 __ __ 12 11| 3
| __ 55 __ __ 02 __ __ 08 *10| 2
| __ __ __ 52 __ 05 __ *07 *09| 1
'-----------------------------------'
a b c d e f g h i
We have reached a key position. How to continue ?
Update (Jul 28, 2025)
7 numbers 60,59,58,57,54,53,51 locked
at 7 cells: a1,a2,b1,c1,c2,d2,e1
22.(51)e1 23.(53)d2 24.(60)c2 25.(57)a2
26.(58)a1 27.(59)b1 28.(54)c1 29.(50)f2
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
|*73 *78 __ 44 __ __ __ 30 *28| 7
|*66 72 *79 45 __ 21 __ 19 *29| 6
|*65 *67 71 *80 __ __ 18 *14 *16| 5
| 64 62 *68 *70 81 __ *13 17 15| 4
| 63 56 *61 *69 01 __ __ 12 11| 3
|*57 55 *60 *53 02 *50 __ 08 *10| 2
|*58 *59 *54 52 *51 05 __ *07 *09| 1
'-----------------------------------'
a b c d e f g h i
30.(3)f3 31.(04)g2 32.(6)g1 33.(49)g3
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
|*73 *78 __ 44 __ __ __ 30 *28| 7
|*66 72 *79 45 __ 21 __ 19 *29| 6
|*65 *67 71 *80 __ __ 18 *14 *16| 5
| 64 62 *68 *70 81 ___*13 17 15| 4
| 63 56 *61 *69 01 *03 *49 12 11| 3
|*57 55 *60 *53 02 *50 *04 08 *10| 2
|*58 *59 *54 52 *51 05 *06 *07 *09| 1
'-----------------------------------'
a b c d e f g h i
34.(48)f4
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
|*73 *78 __ 44 __ __ __ 30 *28| 7
|*66 72 *79 45 __ 21 __ 19 *29| 6
|*65 *67 71 *80 __ __ 18 *14 *16| 5
| 64 62 *68 *70 81 *48 *13 17 15| 4
| 63 56 *61 *69 01 *03 *49 12 11| 3
|*57 55 *60 *53 02 *50 *04 08 *10| 2
|*58 *59 *54 52 *51 05 *06 *07 *09| 1
'-----------------------------------'
a b c d e f g h i
How to finish the puzzle ?
Update (July 30, 2025)
35.(47)f5!
[(47)e5 is not possible: (46)e6 creates a problem to fill f5
with 22,23 and link them to (28)i7 since (20),(31)block the path]
36.(46)e5
,-----------------------------------,
|*76 75 __ __ __ __ __ __ __| 9
|*77 74 __ __ 33 36 __ __ __| 8
|*73 *78 __ 44 __ __ __ 30 *28| 7
|*66 72 *79 45 __ 21 __ 19 *29| 6
|*65 *67 71 *80 *46 *47 18 *14 *16| 5
| 64 62 *68 *70 81 *48 *13 17 15| 4
| 63 56 *61 *69 01 *03 *49 12 11| 3
|*57 55 *60 *53 02 *50 *04 08 *10| 2
|*58 *59 *54 52 *51 05 *06 *07 *09| 1
'-----------------------------------'
a b c d e f g h i
Now, we need a last major deduction to remove the last hurdle.
The hint is to study the correct place for 32.
Update (Jul 31, 2025)
37.(32)f7 would force 38.(20)g6 39.(22)g7! 40.(31)g8 making
impossible to connect 22 to 28.
So, 37.(32)f9! 38.(31)g8 and now there is only one way to
fill out the right-hand side of the puzzle. The remaining
moves are easy. The unique solution is
76 75 41 34 35 32 24 25 26
77 74 42 40 33 36 31 23 27
73 78 43 44 39 37 22 30 28
66 72 79 45 38 21 20 19 29
65 67 71 80 46 47 18 14 16
64 62 68 70 81 48 13 17 15
63 56 61 69 01 03 49 12 11
57 55 60 53 02 50 04 08 10
58 59 54 52 51 05 06 07 09
I could not resist proposing this nice puzzle by Evert).
(king's walk problem with initial and final positions not given).
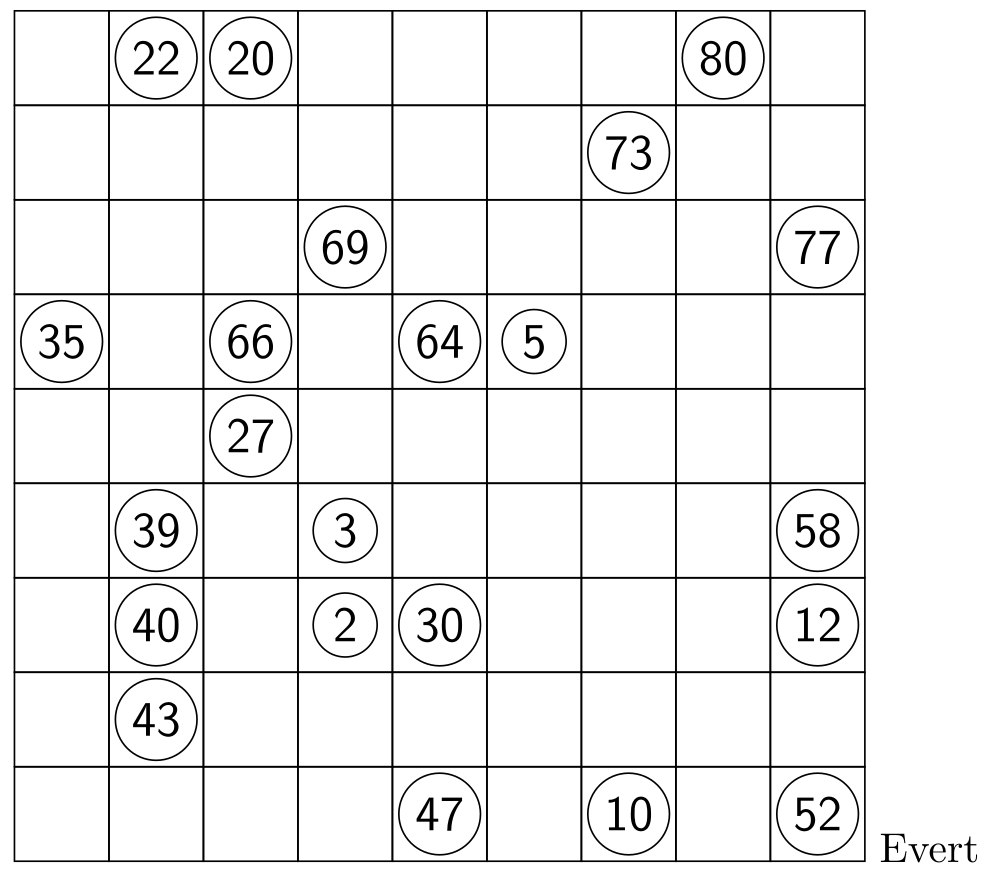
,----------------------------------,
|__ 22 20 __ __ __ __ 80 __| 9
|__ __ __ __ __ __ 73 __ __| 8
|__ __ __ 69 __ __ __ __ 77| 7
|35 __ 66 __ 64 05 __ __ __| 6
|__ __ 27 __ __ __ __ __ __| 5
|__ 39 __ 03 __ __ __ __ 58| 4
|__ 40 __ 02 30 __ __ __ 12| 3
|__ 43 __ __ __ __ __ __ __| 2
|__ __ __ __ 47 __ 10 __ 52| 1
'----------------------------------'
a b c d e f g h i Evert
Update (July 22, 2025)
1.(11)h2 2.(4)e5 3.(28)d5 4.(29)e4 5.(65)d6
,----------------------------------,
|__ 22 20 __ __ __ __ 80 __| 9
|__ __ __ __ __ __ 73 __ __| 8
|__ __ __ 69 __ __ __ __ 77| 7
|35 __ 66 *65 64 05 __ __ __| 6
|__ __ 27 *28 *04 __ __ __ __| 5
|__ 39 __ 03 *29 __ __ __ 58| 4
|__ 40 __ 02 30 __ __ __ 12| 3
|__ 43 __ __ __ __ __ *11 __| 2
|__ __ __ __ 47 __ 10 __ 52| 1
'----------------------------------'
a b c d e f g h i
6.(34)b5! 7.(33)c4 8.(32)c3 9.(31)d2 10.(26)b6
,----------------------------------,
|__ 22 20 __ __ __ __ 80 __| 9
|__ __ __ __ __ __ 73 __ __| 8
|__ __ __ 69 __ __ __ __ 77| 7
|35 *26 66 *65 64 05 __ __ __| 6
|__ *34 27 *28 *04 __ __ __ __| 5
|__ 39 *33 03 *29 __ __ __ 58| 4
|__ 40 *32 02 30 __ __ __ 12| 3
|__ 43 __ *31 __ __ __ *11 __| 2
|__ __ __ __ 47 __ 10 __ 52| 1
'----------------------------------'
a b c d e f g h i
11.(36)a5! 12.(37)a4 13.(38)a3
,-----------------------------------,
| __ 22 20 __ __ __ __ 80 __| 9
| __ __ __ __ __ __ 73 __ __| 8
| __ __ __ 69 __ __ __ __ 77| 7
| 35 *26 66 *65 64 05 __ __ __| 6
|*36 *34 27 *28 *04 __ __ __ __| 5
|*37 39 *33 03 *29 __ __ __ 58| 4
|*38 40 *32 02 30 __ __ __ 12| 3
|*41 43 *01 *31 __ __ __ *11 __| 2
|*42 *44 *45 *46 47 __ 10 __ 52| 1
'-----------------------------------'
a b c d e f g h i
14.(41)a2! 15.(42)a1 16.(44)b1!
17.(46)d1 18.(01)c2! 19.(45)c1
How to proceed ?
Update (Jul 23, 2025)
20.(13)h4!
(h3 can't have 13 because of problems at h1,i2;
i2 can't have 13: it looses connection to 20)
,-----------------------------------,
| __ 22 20 __ __ __ __ 80 __| 9
| __ __ __ __ __ __ 73 __ __| 8
| __ __ __ 69 __ __ __ __ 77| 7
| 35 *26 66 *65 64 05 __ __ __| 6
|*36 *34 27 *28 *04 __ __ __ __| 5
|*37 39 *33 03 *29 __ __ *13 58| 4
|*38 40 *32 02 30 __ __ __ 12| 3
|*41 43 01 *31 __ __ __ *11 __| 2
|*42 *44 *45 *46 47 __ 10 __ 52| 1
'-----------------------------------'
a b c d e f g h i
Now there is only on viable place for 51,
giving 14 more placements and reaching
the last key position of this puzzle.
(Update Jul 24, 2025)
After all placements, we get
,-----------------------------------,
| __ 22 20 __ __ __ __ 80 __| 9
| __ __ __ __ __ __ 73 __ __| 8
| __ __ __ 69 __ __ __ __ 77| 7
| 35 *26 66 *65 64 05 __ __ __| 6
|*36 *34 27 *28 *04 *06 *14 *57 *59| 5
|*37 39 *33 03 *29 *07 *56 *13 58| 4
|*38 40 *32 02 30 *08 *55 *54 12| 3
|*41 43 01 *31 *48 *09 *50 *11 *53| 2
|*42 *44 *45 *46 47 *49 10 *51 52| 1
'-----------------------------------'
a b c d e f g h i
Now, looking carefully at the grid, certain
quantity q of numbers are locked into q places.
This observation basically solves the puzzle.
Update (Jul 26, 2025)
,-----------------------------------,
| x_ 22 20 __ __ __ __ 80 __| 9
| x_ x_ x_ __ __ __ 73 __ __| 8
| x_ x_ x_ 69 __ __ __ __ 77| 7
| 35 *26 66 *65 64 05 __ __ __| 6
|*36 *34 27 *28 *04 *06 *14 *57 *59| 5
|*37 39 *33 03 *29 *07 *56 *13 58| 4
|*38 40 *32 02 30 *08 *55 *54 12| 3
|*41 43 01 *31 *48 *09 *50 *11 *53| 2
|*42 *44 *45 *46 47 *49 10 *51 52| 1
'-----------------------------------'
a b c d e f g h i
Numbers 25,24,23,21,19,67,68 are locked into
the region with locations a7,a8,a9,b7,b8,c7,c8
(marked with x above) and their places are easy
to see:
26.(19)c8 27.(68)c7 28.(21)b8 29.(67)b7
30.(23)a9 31.(24)a8 31.(25)a7
,-----------------------------------,
|*23 22 20 __ __ __ __ 80 __| 9
|*24 *21 *19 __ __ __ 73 __ __| 8
|*25 *67 *68 69 __ __ __ __ 77| 7
| 35 *26 66 *65 64 05 __ __ __| 6
|*36 *34 27 *28 *04 *06 *14 *57 *59| 5
|*37 39 *33 03 *29 *07 *56 *13 58| 4
|*38 40 *32 02 30 *08 *55 *54 12| 3
|*41 43 01 *31 *48 *09 *50 *11 *53| 2
|*42 *44 *45 *46 47 *49 10 *51 52| 1
'-----------------------------------'
a b c d e f g h i
32.(15)g6! and easy singles to the end.
23 22 20 18 71 72 81 80 79
24 21 19 70 17 62 73 74 78
25 67 68 69 63 16 61 75 77
35 26 66 65 64 5 15 60 76
36 34 27 28 4 6 14 57 59
37 39 33 3 29 7 56 13 58
38 40 32 2 30 8 55 54 12
41 43 1 31 48 9 50 11 53
42 44 45 46 47 49 10 51 52
I propose the following Hidoku puzzle (my fourth creation!).
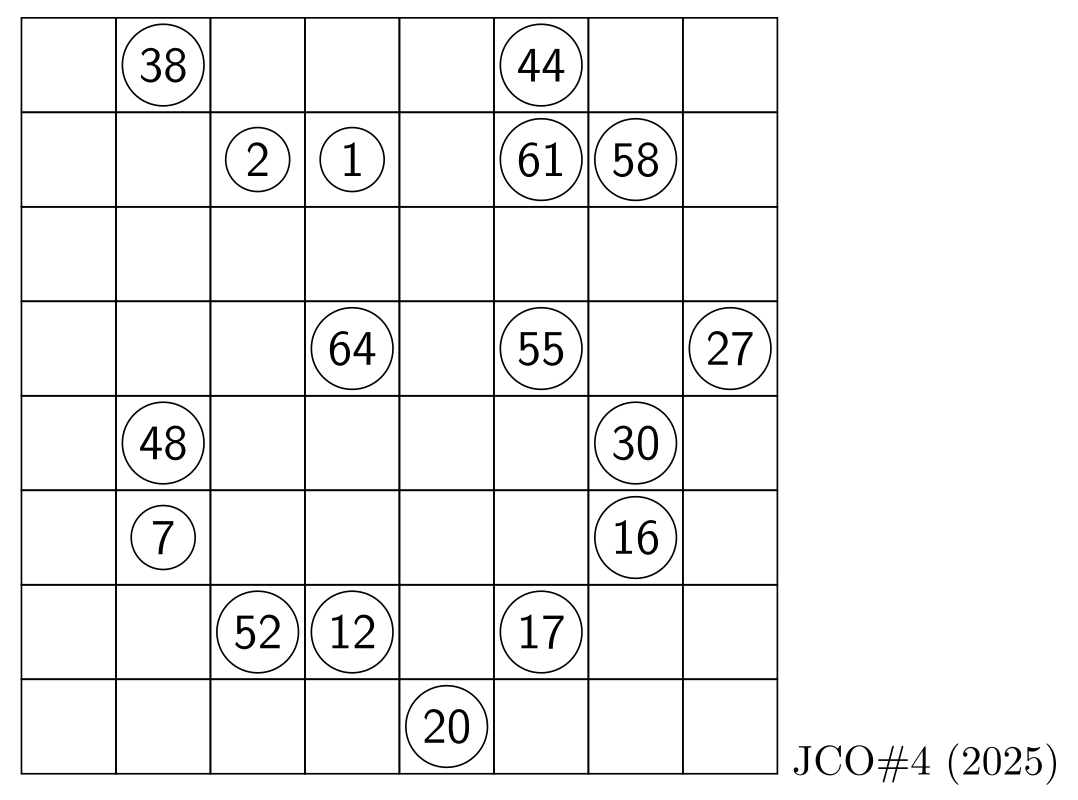
Grid with givens
,-------------------------------,
|__ 38 __ __ __ 44 __ __ | 8
|__ __ 02 01 __ 61 58 __ | 7
|__ __ __ __ __ __ __ __ | 6
|__ __ __ 64 __ 55 __ 27 | 5
|__ 48 __ __ __ __ 30 __ | 4
|__ 07 __ __ __ __ 16 __ | 3
|__ __ 52 12 __ 17 __ __ | 2
|__ __ __ __ 20 __ __ __ | 1
'-------------------------------'
a b c d e f g h JCO#4 (Hidoku)
Update (Oct 22, 2025)
At the start, the path from 44 to 48, and 52 to 54 are clear.
Also the top-left part is easily solved.
,--------------------------------,
|*39 38 *41 *42 *43 44 __ __ | 8
|*37 *40 02 01 *45 61 58 __ | 7
| __ __ __ *46 __ __ __ __ | 6
| __ __ *47 64 __ 55 __ 27 | 5
| __ 48 __ __ *54 __ 30 __ | 4
| __ 07 __ *53 __ __ 16 __ | 3
| __ __ 52 12 __ 17 __ __ | 2
| __ __ __ __ 20 __ __ __ | 1
'--------------------------------'
a b c d e f g h
How to continue ?
Update (Oct 23, 2025)
. path from 30 to 37
. path from 02 to 07
,--------------------------------,
|*39 38 *41 *42 *43 44 __ __ | 8
|*37 *40 02 01 *45 61 58 __ | 7
|*36 *04 *03 *46 __ __ __ __ | 6
|*05 *35 *47 64 __ 55 __ 27 | 5
|*06 48 *34 *33 *54 __ 30 __ | 4
| __ 07 __ *53 __ __ 16 __ | 3
| __ __ 52 12 __ 17 __ __ | 2
| __ __ __ __ 20 __ __ __ | 1
'--------------------------------'
a b c d e f g h
Now, how to make progress from here ?
EDIT: corrected configuration.
Update (Oct 24, 2025)
. (49)c3 implies (50)b2 that leaves a1 empty to connect 07 to 12.
=> 20.(49)a3!
,--------------------------------,
|*39 38 *41 *42 *43 44 __ __ | 8
|*37 *40 02 01 *45 61 58 __ | 7
|*36 *04 *03 *46 __ __ __ __ | 6
|*05 *35 *47 64 __ 55 __ 27 | 5
|*06 48 *34 *33 *54 __ 30 __ | 4
|*49 07 __ *53 __ __ 16 __ | 3
| __ __ 52 12 __ 17 __ __ | 2
| __ __ __ __ 20 __ __ __ | 1
'--------------------------------'
a b c d e f g h
. (50)a2 is not possible because it forces (51)b1 creating a problem at a1, b2
=> 21.(50)b2!, 22.(51)c3
,--------------------------------,
|*39 38 *41 *42 *43 44 __ __ | 8
|*37 *40 02 01 *45 61 58 __ | 7
|*36 *04 *03 *46 __ __ __ __ | 6
|*05 *35 *47 64 __ 55 __ 27 | 5
|*06 48 *34 *33 *54 __ 30 __ | 4
|*49 07 *51 *53 __ __ 16 __ | 3
| __ *50 52 12 __ 17 __ __ | 2
| __ __ __ __ 20 __ __ __ | 1
'--------------------------------'
a b c d e f g h
Now: 23.(08)a2, 24.(09)a1, 25.(10)b1, 26.(11)c1.
,--------------------------------,
|*39 38 *41 *42 *43 44 __ __ | 8
|*37 *40 02 01 *45 61 58 __ | 7
|*36 *04 *03 *46 __ __ __ __ | 6
|*05 *35 *47 64 __ 55 __ 27 | 5
|*06 48 *34 *33 *54 __ 30 __ | 4
|*49 07 *51 *53 __ __ 16 __ | 3
|*08 *50 52 12 __ 17 __ __ | 2
|*09 *10 *11 __ 20 __ __ __ | 1
'--------------------------------'
a b c d e f g h
How to continue from here ?
Update (Oct 25, 2025)
. (13)c1 -> (14)e2, and now we have a problem: (20)e1.
. (21)d1 -> (22)e2, (13)e3, (19)f1, (23)f3 and
now f4 is needed for (14) and (31) simultaneously.
=> 27.(19)d1 !! and from here singles to the end.
I propose the following (tough!) Hidoku puzzle to be solved manually.
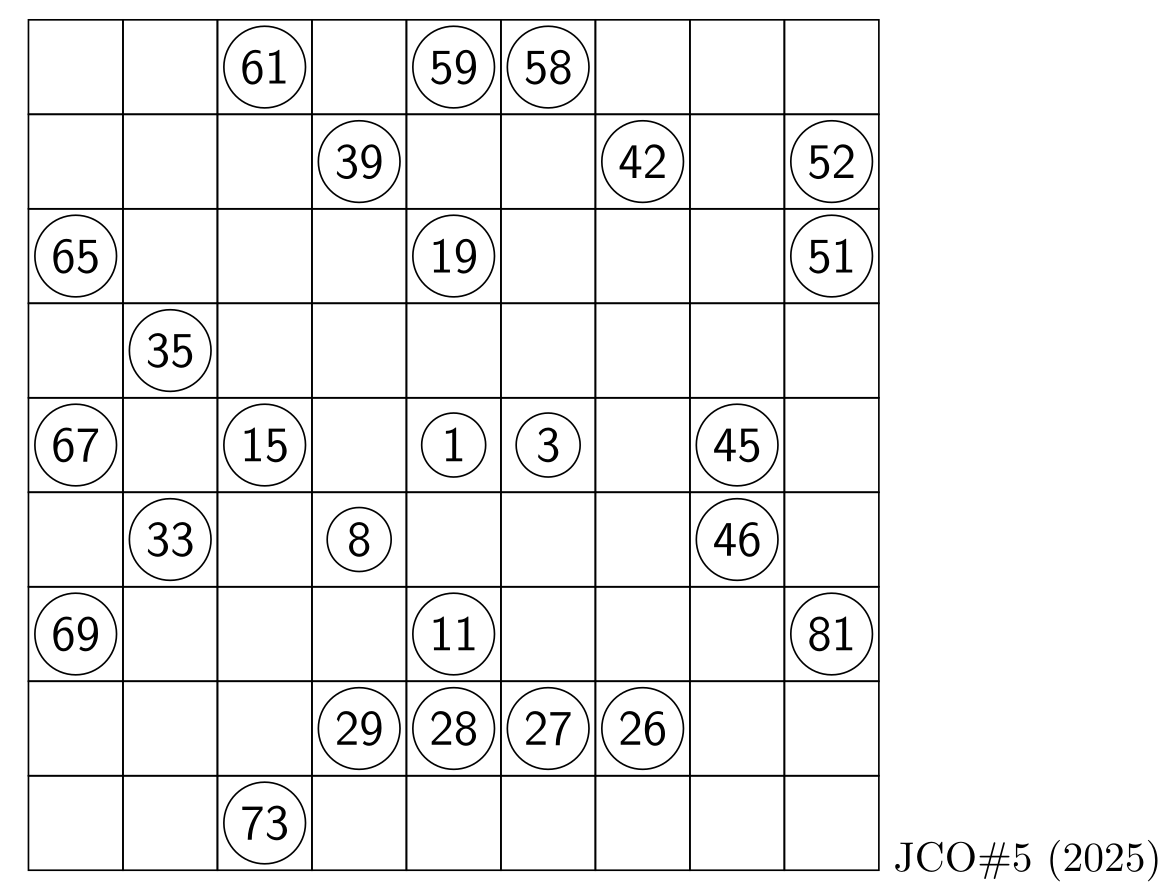
,----------------------------------,
|__ __ 61 __ 59 58 __ __ __| 9
|__ __ __ 39 __ __ 42 __ 52| 8
|65 __ __ __ 19 __ __ __ 51| 7
|__ 35 __ __ __ __ __ __ __| 6
|67 __ 15 __ 01 03 __ 45 __| 5
|__ 33 __ 08 __ __ __ 46 __| 4
|69 __ __ __ 11 __ __ __ 81| 3
|__ __ __ 29 28 27 26 __ __| 2
|__ __ 73 __ __ __ __ __ __| 1
'----------------------------------'
a b c d e f g h i JCO#5 (Hidoku)
Update (Oct 28, 2025)
Step 1: 5 immediate placements.
,-----------------------------------,
| __ __ 61 *60 59 58 __ __ __| 9
| __ __ __ 39 *40 __ 42 __ 52| 8
| 65 __ __ __ 19 __ __ __ 51| 7
|*66 35 __ __ __ __ __ __ __| 6
| 67 *34 15 __ 01 03 __ 45 __| 5
|*68 33 __ 08 __ __ __ 46 __| 4
| 69 __ __ __ 11 __ __ __ 81| 3
| __ __ __ 29 28 27 26 __ __| 2
| __ __ 73 __ __ __ __ __ __| 1
'-----------------------------------'
a b c d e f g h i
Now, for the next number, further analysis
is required to make progress.
Update (Oct 29, 2025)
Step 2:
. We first notice that we can't have
e3,d4 both used for the path (12-13-14) because
it would block any possible path from 01 to 08.
=> * 12 can't go to f3 or f4 *
Now, either (12)d3 or (12)e4 is true.
BUT (12) e4 blocks the path 01-08, because
from above, (12)e4 -> (13)d2, (14)c3
=> 6.(12)d3!! and several placements follow
,-----------------------------------,
| __ __ 61 *60 59 58 __ __ __| 9
| __ __ __ 39 *40 __ 42 __ 52| 8
| 65 __ __ __ 19 __ __ __ 51| 7
|*66 35 __ __ __ __ __ __ __| 6
| 67 *34 15 __ 01 03 __ 45 __| 5
|*68 33 __ 08 __ __ __ 46 __| 4
| 69 __ __ *12 11 __ __ __ 81| 3
| __ __ __ 29 28 27 26 __ __| 2
| __ __ 73 __ __ __ __ __ __| 1
'-----------------------------------'
a b c d e f g h i
Update (Oct 31, 2025)
7.(14)c3! 8.(13)c3 9.(32)b3 10.(30)c2
11.(31)b2, 12.(70)a2, 13.(71)a1, 14.(72)b1
15.(74)d1, 16.(75)e1, 17.(76)f1, 18.(77)g1
19.(07)d5, 20.(09)e4 and we reach the following
,-----------------------------------,
| __ __ 61 *60 59 58 __ __ __| 9
| __ __ __ 39 *40 __ 42 __ 52| 8
| 65 __ __ __ 19 __ __ __ 51| 7
|*66 35 __ __ __ __ __ __ __| 6
| 67 *34 15 *07 01 03 __ 45 __| 5
|*68 33 *14 08 *09 __ __ 46 __| 4
| 69 *32 *13 *12 11 __ __ __ 81| 3
|*70 *31 *30 29 28 27 26 __ __| 2
|*71 *72 73 *74 *75 *76 *77 __ __| 1
'-----------------------------------'
a b c d e f g h i
How to continue ?
Update (Nov 1, 2025)
Clearly, the sole passage e6 is the key, being
critical to the path 01-07. There are 9 numbers
confined into 10 cells and a key inference from
this observation basically solves the puzzle.
Update(Nov 2, 2025)
the 9 numbers 64,63,62,38,37,36,18,17,16
are confined into the 10-cells region:
a8, a9, b7, b8, b9, c6, c7, c8, d6, d7.
So 21.(06)d6!! and this gives 13 placements
to reach
,-----------------------------------,
|*63 *62 61 *60 59 58 __ __ __| 9
|*64 *37 *38 39 *40 __ 42 __ 52| 8
| 65 *36 *17 *18 19 __ __ __ 51| 7
|*66 35 *16 *06 *05 *04 __ __ __| 6
| 67 *34 15 *07 01 03 __ 45 __| 5
|*68 33 *14 08 *09 *02 __ 46 __| 4
| 69 *32 *13 *12 11 *10 __ __ 81| 3
|*70 *31 *30 29 28 27 26 __ __| 2
|*71 *72 73 *74 *75 *76 *77 __ __| 1
'-----------------------------------'
a b c d e f g h i
Since numbers 20,41 are locked into f7,f8,
we can advance easily solving the puzzle.
This new Hidoku puzzle ("Tightly tied knot ?") has an easy start, but becomes tough later.
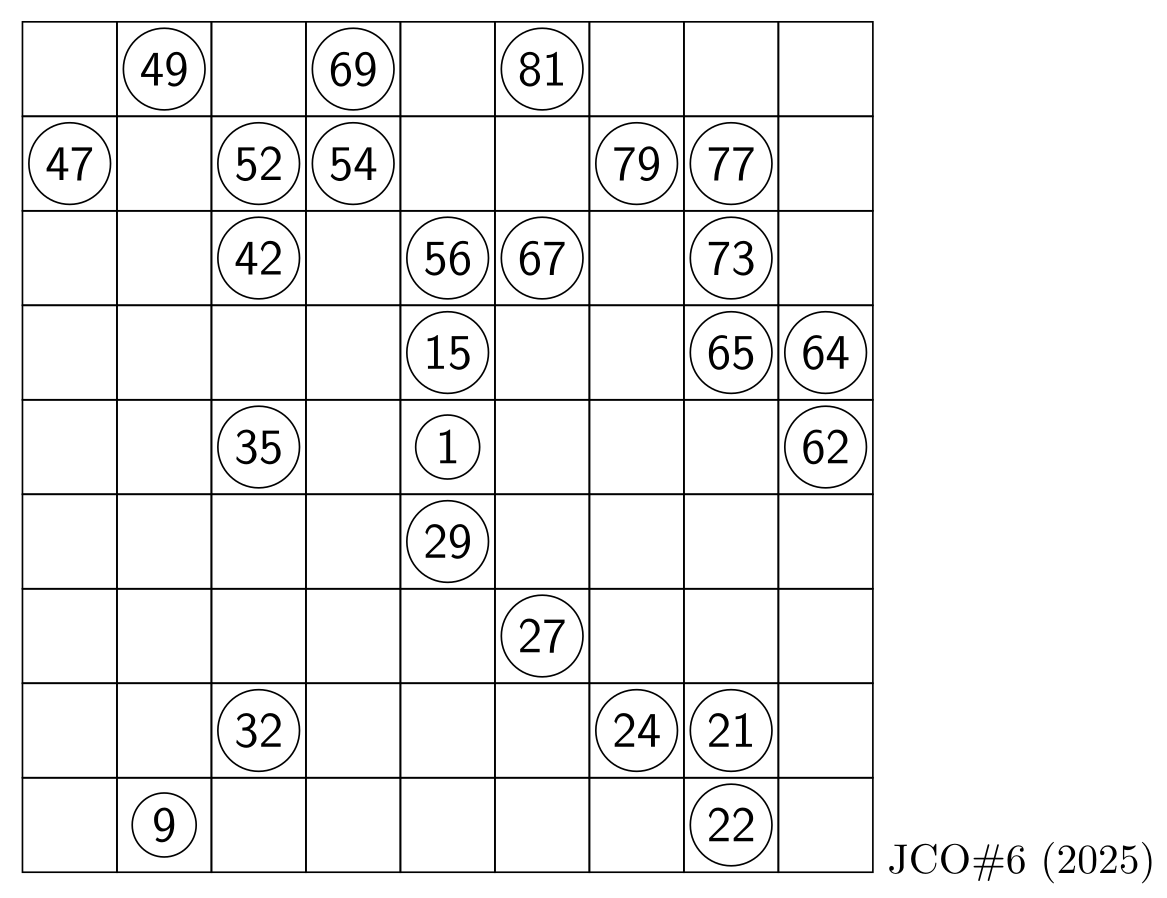
,------------------------------------,
| __ 49 __ 69 __ 81 __ __ __ | 9
| 47 __ 52 54 __ __ 79 77 __ | 8
| __ __ 42 __ 56 67 __ 73 __ | 7
| __ __ __ __ 15 __ __ 65 64 | 6
| __ __ 35 __ 01 __ __ __ 62 | 5
| __ __ __ __ 29 __ __ __ __ | 4
| __ __ __ __ __ 27 __ __ __ | 3
| __ __ 32 __ __ __ 24 21 __ | 2
| __ 09 __ __ __ __ __ 22 __ | 1
'------------------------------------'
a b c d e f g h i JCO#6 (Hidoku)
Update (Nov 6, 2025)
After 28 placements:
,------------------------------------,
|*48 49 *53 69 *70 81 *80 *78 *76 | 9
| 47 *50 52 54 *68 *71 79 77 *75 | 8
|*46 *51 42 *55 56 67 *72 73 *74 | 7
| __ __ __ __ 15 *57 *66 65 64 | 6
| __ __ 35 __ 01 *16 *58 *63 62 | 5
| __ __ __ __ 29 __ *17 *59 *61 | 4
| __ __ __ __ __ 27 __ *18 *60 | 3
| __ __ 32 __ __ __ 24 21 *19 | 2
| __ 09 __ __ __ __ *23 22 *20 | 1
'------------------------------------'
a b c d e f g h i
The puzzle is locked! How to proceed from here ?
Update (Nov 7, 2025)
Analyze which of the two possibilities for placing 14 is false.
Notice that (14)d6 restricts a lot rows 3,4,5,6.
Update (Nov 8, 2025)
So, a careful analysis of the consequences of (14)d6 leads to
. Three numbers (41,43,45) locked into three cells (a6,b6,c6)
. Two numbers (40,44) locked into two cells (a5,b5)
. Four number (12,34,36,39) locked into four cells (a4,b4,c4,d4)
. Six numbers (03,11,28,33,37,38) locked into six cells (a3,b3,c3,d3,e3,g3)
Now, notice that there is no place for the number 30!
=> 29. (14)d5!!
,------------------------------------,
|*48 49 *53 69 *70 81 *80 *78 *76 | 9
| 47 *50 52 54 *68 *71 79 77 *75 | 8
|*46 *51 42 *55 56 67 *72 73 *74 | 7
| __ __ __ __ 15 *57 *66 65 64 | 6
| __ __ 35 *14 01 *16 *58 *63 62 | 5
| __ __ __ __ 29 __ *17 *59 *61 | 4
| __ __ __ __ __ 27 __ *18 *60 | 3
| __ __ 32 __ __ __ 24 21 *19 | 2
| __ 09 __ __ __ __ *23 22 *20 | 1
'------------------------------------'
a b c d e f g h i
This move does not give immediate placements,
but now one can ask: which numbers go to c6,d6 ?
Update (Nov 9, 2025)
. 41,43,45 are locked into row 6 [45 at a6/b6, 41,43 at b6/c6/d6]
. 40,44 must be located at row 5 or 6.
. The numbers at c6,d6,c7 must be consecutive to comply with the "corner" d6.
=> 30. (41)!!d6
[and 5 placements: 31.(40)c6, 32.(43)b6, 33. (45)a6, 34.(39)b5, 35.(44)a4 ]
,------------------------------------,
|*48 49 *53 69 *70 81 *80 *78 *76 | 9
| 47 *50 52 54 *68 *71 79 77 *75 | 8
|*46 *51 42 *55 56 67 *72 73 *74 | 7
|*45 *43 *40 *41 15 *57 *66 65 64 | 6
|*44 *39 35 *14 01 *16 *58 *63 62 | 5
| __ __ __ __ 29 __ *17 *59 *61 | 4
| __ __ __ __ __ 27 __ *18 *60 | 3
| __ __ 32 __ __ __ 24 21 *19 | 2
| __ 09 __ __ __ __ *23 22 *20 | 1
'------------------------------------'
a b c d e f g h i
Is the knot untied ?
Update (Nov 10, 2025)
,------------------------------------,
|*48 49 *53 69 *70 81 *80 *78 *76 | 9
| 47 *50 52 54 *68 *71 79 77 *75 | 8
|*46 *51 42 *55 56 67 *72 73 *74 | 7
|*45 *43 *40 *41 15 *57 *66 65 64 | 6
|*44 *39 35 *14 01 *16 *58 *63 62 | 5
| __ __ __ __ 29 __ *17 *59 *61 | 4 02,13,34,36,38 [locked!]
| __ __ __ __ __ 27 __ *18 *60 | 3 33,28,30
| __ __ 32 __ __ __ 24 21 *19 | 2
| __ 09 __ __ __ __ *23 22 *20 | 1
'------------------------------------'
a b c d e f g h i
(02,13,34,36,38) are locked into row 4 with (02)f4 forced,
and there are only two possible places for 28: e3, f4,
=> 36.(02)f4!, 37.(28)e3!, 38.(03)g3, 39.(04)f2, 40.(25)f1,
41.(30)d3! (since d4 is taken!) 42.(26)e2, 43.(05)e1
,------------------------------------,
|*48 49 *53 69 *70 81 *80 *78 *76 | 9
| 47 *50 52 54 *68 *71 79 77 *75 | 8
|*46 *51 42 *55 56 67 *72 73 *74 | 7
|*45 *43 *40 *41 15 *57 *66 65 64 | 6
|*44 *39 35 *14 01 *16 *58 *63 62 | 5
| __ __ __ __ 29 *02 *17 *59 *61 | 4 13,34,36,38 [locked!]
| __ __ __ *30 *28 27 *03 *18 *60 | 3 33
| __ __ 32 __ *26 *04 24 21 *19 | 2
| __ 09 __ __ *05 *25 *23 22 *20 | 1
'------------------------------------'
a b c d e f g h i
Now it is almost over! what would be a final move ?
Update Nov 11, 2025
,------------------------------------,
|*48 49 *53 69 *70 81 *80 *78 *76 | 9
| 47 *50 52 54 *68 *71 79 77 *75 | 8
|*46 *51 42 *55 56 67 *72 73 *74 | 7
|*45 *43 *40 *41 15 *57 *66 65 64 | 6
|*44 *39 35 *14 01 *16 *58 *63 62 | 5
| __ __ __ __ 29 *02 *17 *59 *61 | 4 13,34,36,38 [locked!]
| __ __ __ *30 *28 27 *03 *18 *60 | 3 12,33,37 [locked!]
| __ __ 32 __ *26 *04 24 21 *19 | 2 31 only place is d2
| __ 09 __ __ *05 *25 *23 22 *20 | 1
'------------------------------------'
a b c d e f g h i
44.(31)d2! (see comments at side of the grid) and now only singles remain.
48 49 53 69 70 81 80 78 76
47 50 52 54 68 71 79 77 75
46 51 42 55 56 67 72 73 74
45 43 40 41 15 57 66 65 64
44 39 35 14 1 16 58 63 62
38 36 13 34 29 2 17 59 61
37 12 33 30 28 27 3 18 60
11 8 32 31 26 4 24 21 19
10 9 7 6 5 25 23 22 20
This new Hidoku puzzle is quite different from HP#8: the difficulties
in the puzzle are present only at the start. After something is
noticed (proved), the solution is smooth to the end.
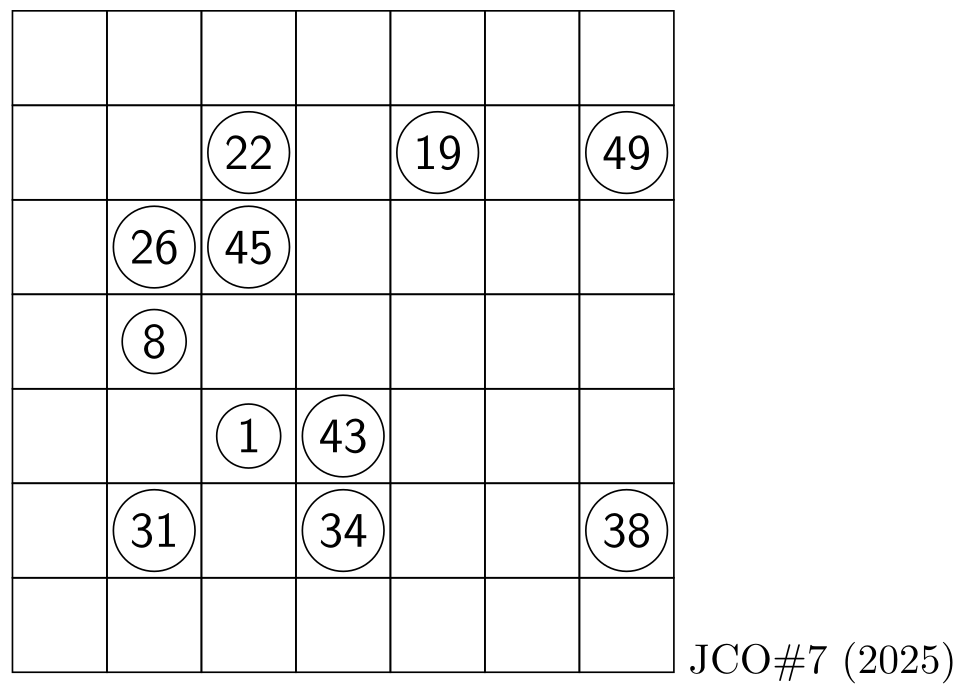
,-----------------------------,
| __ __ __ __ __ __ __ | 7
| __ __ 22 __ 19 __ 49 | 6
| __ 26 45 __ __ __ __ | 5
| __ 08 __ __ __ __ __ | 4
| __ __ 01 43 __ __ __ | 3
| __ 31 __ 34 __ __ 38 | 2
| __ __ __ __ __ __ __ | 1
'-----------------------------'
a b c d e f g JCO#7
Updated (Dec 28, 2025)
The natural place to start is to find the
right spot for the number 44 (2 possibilities).
One must show that (44)d4 is false. After that
and an observation that comes for free from the
analysis, the remaning 37 moves are easily found.
Update (Dec 30, 2025)
Part 1 [of analysis]:
We consider the possibility of 1. (44)d4
46 47 48
,-----------------------------,
| __ __ __ __ __ __ __ | 7
| __ __ 22 __ 19 __ 49 | 6
| __ 26 45 __ __ __ __ | 5
| __ 08 __ 44? __ __ __ | 4
| __ __ 01 43 __ __ __ | 3
| __ 31 __ 34 __ __ 38 | 2
| __ __ __ __ __ __ __ | 1
'-----------------------------'
a b c d e f g JCO#7
Part 1.1:
within the possibility of 1.(44)d4,
we consider the possibility of 2.(47)e7 3.(46)d6.
48
,-----------------------------,
| __ __ __ __ 47? __ __ | 7
| __ __ 22 46? 19 __ 49 | 6
| __ 26 45 __ __ __ __ | 5
| __ 08 __ 44? __ __ __ | 4
| __ __ 01 43 __ __ __ | 3
| __ 31 __ 34 __ __ 38 | 2
| __ __ __ __ __ __ __ | 1
'-----------------------------'
a b c d e f g JCO#7
We want to see if this configuration
leads to a contradiction in order
to discard this possibility of 2.(47)e7.
How can we show this ?
Update (Dec 31, 2025)
The analysis for this possibility will be shown
next. Similar analysis for the other two
possibilities (1.(44)d4 2.(47)e5 3.(46)d5/d6 is
the second possibility and 1.(44)d4 2.(47)e4 3.(46)d5
is the third possibility) will be omitted because it
contains similar ideas.
Analysis for the first possibility:
If we connect 08 -> 19 using cells c4,d5,
then 19 -> 22 must use cells c7,d7. Now,
22 -> 26 and 26->31 must use cells b6,b7,
a7,a6,a5,a4, and a3|b3. Then a3|b3 must
be used for the path 01 -> 08, but this
path gets in the way of the path 31 -> 34.
(here | denotes "or")
,-----------------------------,
| zz zz yy yy 47? __ __ | 7
| zz zz 22 46? 19 __ 49 | 6
| zz 26 45 xx __ __ __ | 5
| zz 08 xx 44? __ __ __ | 4
| z_ z_ 01 43 __ __ __ | 3
| __ 31 __ 34 __ __ 38 | 2
| __ __ __ __ __ __ __ | 1
'-----------------------------'
a b c d e f g JCO#7
After all three possibilites are discarded
as leading to impossible situations, we
finally have a first move!
1.(44)c4!!
,-----------------------------,
| __ __ __ __ __ __ __ | 7
| __ __ 22 __ 19 __ 49 | 6
| __ 26 45 __ __ __ __ | 5
| __ 08 *44 __ __ __ __ | 4
| __ __ 01 43 __ __ __ | 3
| __ 31 __ 34 __ __ 38 | 2
| __ __ __ __ __ __ __ | 1
'-----------------------------'
a b c d e f g JCO#7
How to continue ?
Just one more idea unlocks the puzzle
with singles to the end.
Update (Jan 01, 2026)
Now: if (02)c2|(02)b3, the path 01 -> 08
must to through cells b3,c2,b1,a1,a2,a3
(marked with xx in the grid), blocking
the connection 26->31.
,-----------------------------,
| __ __ __ __ __ __ __ | 7
| __ __ 22 __ 19 __ 49 | 6
| __ 26 45 __ __ __ __ | 5
| __ 08 *44 __ __ __ __ | 4
| xx xx 01 43 __ __ __ | 3
| xx 31 xx 34 __ __ 38 | 2
| xx xx __ __ __ __ __ | 1
'-----------------------------'
a b c d e f g JCO#7
So: 2.(02)d4!!
,-----------------------------,
| __ __ __ __ __ __ __ | 7
| __ __ 22 __ 19 __ 49 | 6
| __ 26 45 __ __ __ __ | 5
| __ 08 *44 *02 __ __ __ | 4
| __ __ 01 43 __ __ __ | 3
| __ 31 __ 34 __ __ 38 | 2
| __ __ __ __ __ __ __ | 1
'-----------------------------'
a b c d e f g JCO#7
The (03) location is still undetermined,
but the locations for 04,05,06,07 are
determined. From this, the puzzle is
unlocked and the remaining numbers
can be found easily.
This Hidoku puzzle was created after great modifications from a previous version
with (designed) complex solving path. The modifications were made to circunvent
non-uniqueness issues at the end of the solving path. The resulting puzzle is easier
to solve than I intended, but hopefully it is a good enough challenge.
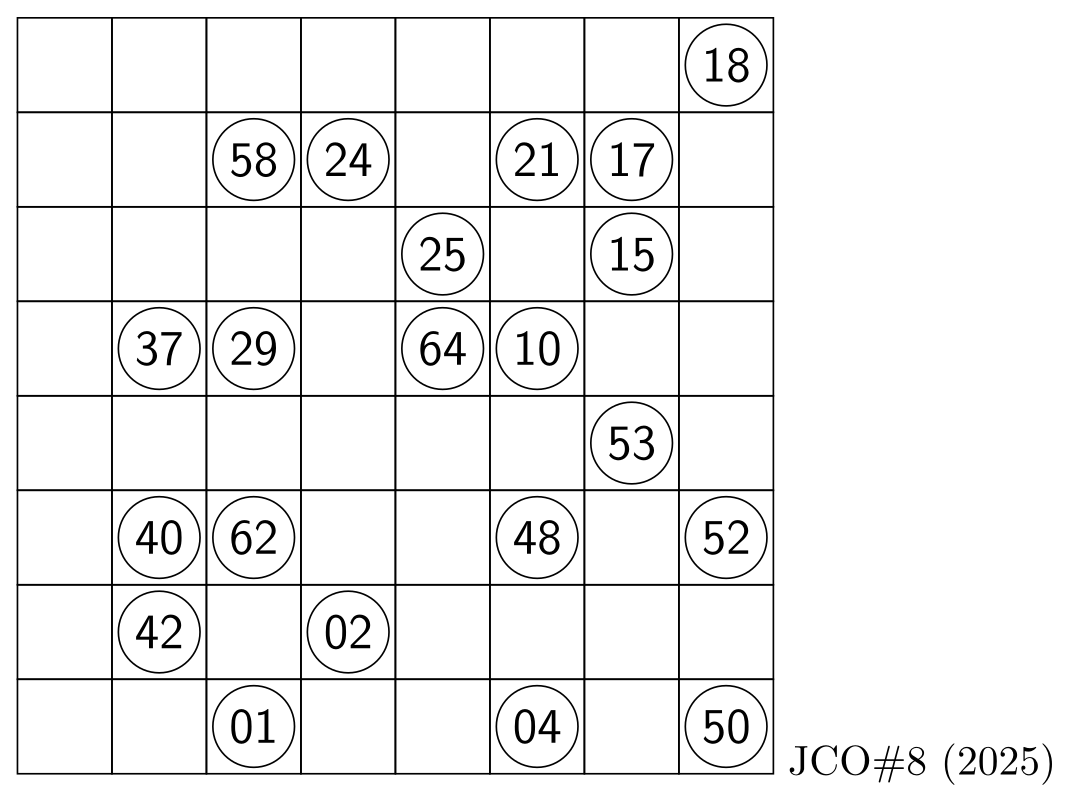
Oops! (forgot to include ascii grid! Done below)
,--------------------------------,
| __ __ __ __ __ __ __ 18 | 8
| __ __ 58 24 __ 21 17 __ | 7
| __ __ __ __ 25 __ 15 __ | 6
| __ 37 29 __ 64 10 __ __ | 5
| __ __ __ __ __ __ 53 __ | 4
| __ 40 62 __ __ 48 __ 52 | 3
| __ 42 __ 02 __ __ __ __ | 2
| __ __ 01 __ __ 04 __ 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
Update (Dec 28, 2025)
We have easy moves at the start:
1.(49)g2 2.(51)h2 3.(05)g1! 4.(06)f2
5.(03)e1! 6.(63)d4
,--------------------------------,
| __ __ __ __ __ __ __ 18 | 8
| __ __ 58 24 __ 21 17 __ | 7
| __ __ __ __ 25 __ 15 __ | 6
| __ 37 29 __ 64 10 __ __ | 5
| __ __ __ *63 __ __ 53 __ | 4
| __ 40 62 __ __ 48 __ 52 | 3
| __ 42 __ 02 __ *06 *49 *51 | 2
| __ __ 01 __ *03 04 *05 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
How to continue ?
Update (Dec 29, 2025)
57
,--------------------------------,
| __ __ __ __ __ __ __ 18 | 8
| __ __ 58 24 __ 21 17 __ | 7
| __ __ __ __ 25 __ 15 __ | 6
| __ 37 29 __ 64 10 __ __ | 5
| __ __ __ *63 __ __ 53 __ | 4
| __ 40 62 __ __ 48 __ 52 | 3
| __ 42 __ 02 __ *06 *49 *51 | 2
| __ __ 01 __ *03 04 *05 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
7.(54)f4 8.(55)e4 9.(56)d5 forces the
path 06 -> 10 to go through cells g3,h4,g5.
That makes the path from 10 to 15 impossible!
So,
7.(54)g5!! 8.(55)f6 9.(56)e7
57
,--------------------------------,
| __ __ __ __ __ __ __ 18 | 8
| __ __ 58 24 *56 21 17 __ | 7
| __ __ __ __ 25 *55 15 __ | 6
| __ 37 29 __ 64 10 *54 __ | 5
| __ __ __ *63 __ __ 53 __ | 4
| __ 40 62 __ __ 48 __ 52 | 3
| __ 42 __ 02 __ *06 *49 *51 | 2
| __ __ 01 __ *03 04 *05 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
What is the right place for 57 ? How to continue ?
Update (Dec 30, 2025)
If 10.(57)d6, then 11. (26)d5 and the path from
26 to 29 gets in the way of the path from 58 to 62.
So,
10.(57)d8!!
,--------------------------------,
| __ __ __ *57 __ __ __ 18 | 8
| __ __ 58 24 *56 21 17 __ | 7
| __ __ __ __ 25 *55 15 __ | 6 . 59
| __ 37 29 __ 64 10 *54 __ | 5 . 60
| __ __ __ *63 __ __ 53 __ | 4 . 09, 61
| __ 40 62 __ __ 48 __ 52 | 3
| __ 42 __ 02 __ *06 *49 *51 | 2
| __ __ 01 __ *03 04 *05 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
Now 10 placements are available and
we reach easily
46 47
26 07
,--------------------------------,
| __ __ __ *57 *23 *22 *20 18 | 8
| __ __ 58 24 *56 21 17 *19 | 7
| __ __ __ __ 25 *55 15 *16 | 6 . 59
| __ 37 29 __ 64 10 *54 *14 | 5 . 60
| __ __ __ *63 *09 *11 53 *13 | 4 . 61
| __ 40 62 __ __ 48 *12 52 | 3 . 08
| __ 42 __ 02 __ *06 *49 *51 | 2
| __ __ 01 __ *03 04 *05 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
How to make progress now ?
Update (Dec 31, 2025)
07,47 are locked into e2,e3 and 08 must go
into one of the cells e2,e3,d3, so
21.(08)d3! 22.(47)e2! 23.(07)e3 and five
more placements lead to
26
,--------------------------------,
| __ __ __ *57 *23 *22 *20 18 | 8
| __ __ 58 24 *56 21 17 *19 | 7
| __ __ __ __ 25 *55 15 *16 | 6 . 59
| __ 37 29 __ 64 10 *54 *14 | 5 . 60
| __ __ __ *63 *09 *11 53 *13 | 4 . 61
| __ 40 62 *08 *07 48 *12 52 | 3
|*41 42 *45 02 *47 *06 *49 *51 | 2
|*43 *44 01 *46 *03 04 *05 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
How to continue ?
Update (Jan 02, 2026)
29.(59)b6!!
[using the route through d5,c4 to connect
58 to 62 gets in the way of the path from
25 to 29, in particular, there is no place for 27]
after two more placements we get
26
,--------------------------------,
| __ __ __ *57 *23 *22 *20 18 | 8
| __ __ 58 24 *56 21 17 *19 | 7
| __ *59 __ __ 25 *55 15 *16 | 6
|*60 37 29 __ 64 10 *54 *14 | 5
| __ *61 __ *63 *09 *11 53 *13 | 4
| __ 40 62 *08 *07 48 *12 52 | 3
|*41 42 *45 02 *47 *06 *49 *51 | 2
|*43 *44 01 *46 *03 04 *05 50 | 1
'--------------------------------'
a b c d e f g h JCO#8
and from here the fact that 26,27,28,29
are locked into the region c4,c6,d5,d6
solves the puzzle with singles.
This newly created Hidoku puzzle is a good challenge: tough to solve manually!
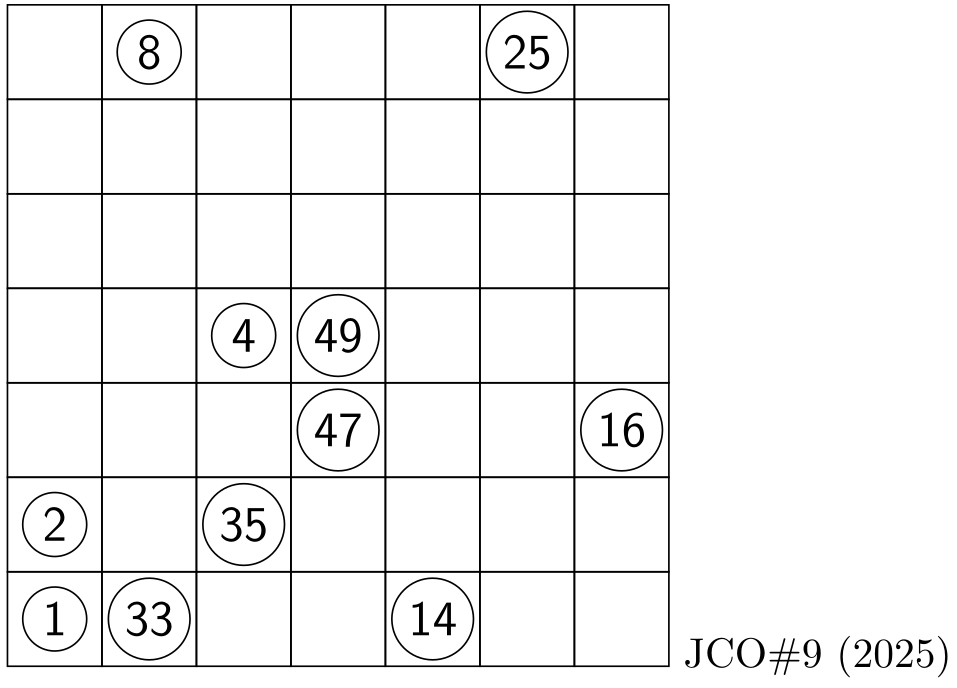
,-----------------------------,
| __ _8 __ __ __ 25 __ | 7
| __ __ __ __ __ __ __ | 6
| __ __ __ __ __ __ __ | 5
| __ __ _4 49 __ __ __ | 4
| __ __ __ 47 __ __ 16 | 3
| _2 __ 35 __ __ __ __ | 2
| _1 33 __ __ 14 __ __ | 1
'-----------------------------'
a b c d e f g JCO#9 (Hidoku)
Update 1 (Jan 31, 2026)
We have two easy numbers 1.(3)b3 2.(15)f2
but no immediate number is available.
,-----------------------------,
| __ 08 __ __ __ 25 __ | 7
| __ __ __ __ __ __ __ | 6
| __ __ __ __ __ __ __ | 5
| __ __ 04 49 __ __ __ | 4
| __ *03 __ 47 __ __ 16 | 3
| 02 __ 35 __ __ *15 __ | 2
| 01 33 __ __ 14 __ __ | 1
'-----------------------------'
a b c d e f g JCO#9 (Hidoku)
A few observations help a lot in the
following steps. Can you list them ?
Update 2 (Feb 1, 2026)
List of observations for this tough puzzle:
A. 32,34 are locked in b2, c1
B. (obvious but very relevant) the path from
08 to 14 must go either above the 'pack'
(04)c4,(49)d4,(47)d3, or passing through
the narrow passage b4,c3,d2.
C. keep in mind the possible paths from 25 to *32*
D. 48 has only three possible places
E. 36 has only three possible places
The key features can be notated as
,-----------------------------,
| __ 08 __ __ __ 25 __ | 7
| __ __ __ __ __ __ __ | 6 ...09 (9 somewhere in row 6)
| __ __ __ __ __ __ __ | 5 ...10 (10 somewhere in row 5)
| __ __ 04 49 __ __ __ | 4 ...11
| __ *03 __ 47 __ __ 16 | 3 ...12
| 02 ww 35 __ __ *15 __ | 2 ...13
| 01 33 ww __ 14 __ __ | 1 ...'ww': 32,34 are locked in b2, c1
'-----------------------------'
a b c d e f g JCO#9
Now, one needs to find a good start.
The hint is to consider E, taking into account A, B.
Update 3 (Fev 2, 2026)
Part 1: We analyse the correct place for 36.
If (36)c3, then the path from 08 to 14 is clear:
(09)c6,(10)d5,(11)e4,(48)e3, (12)f3,(13)e2 and
we have a problem in f1, g1,g2, being
forced to have (17)g2 breaking the connection
to 25. Similar situation occurs with (36)d2,
this time under the fact that 46,48 are locked
in c3.e3. So,
3.(36)d1 !!
,-----------------------------,
| __ 08 __ __ __ 25 __ | 7
| __ __ __ __ __ __ __ | 6 ...09 (9 somewhere in row 6)
| __ __ __ __ __ __ __ | 5 ...10 (10 somewhere in row 5)
| __ __ 04 49 __ __ __ | 4 ...11
| __ *03 __ 47 __ __ 16 | 3 ...12
| 02 ww 35 zz zz *15 __ | 2 ...'zz': 13,37 locked in d2.e2
| 01 33 ww *36 14 __ __ | 1 ...'ww': 32,34 locked in b2, c1
'-----------------------------'
a b c d e f g JCO#9
How to continue ?
Update 4 (Fev 3, 2026)
Part 2: 4.(37)e2! 5.(13)d2
is a consequence of the previous analysis
[(i) (37)d2 would block the path from 08 to 14
going through b4,c3, (ii) c3,e3 must have 46, 48,
so (12)f4, (13)e2 are forced, giving that same
disconnection]
,-----------------------------,
| __ 08 __ __ __ 25 __ | 7
| __ __ __ __ __ __ __ | 6 ...09 (9 somewhere in row 6)
| __ __ __ __ __ __ __ | 5 ...10 (10 somewhere in row 5)
| __ __ 04 49 __ __ __ | 4 ...11
| __ *03 __ 47 __ __ 16 | 3 ...12
| 02 ww 35 *13 *37 *15 __ | 2
| 01 33 ww *36 14 __ __ | 1 ...'ww': 32,34 locked in b2, c1
'-----------------------------'
a b c d e f g JCO#9
Next we ask where 12 goes. Answering this gives 12 placements,
filling out half of the grid.
Update 5 (Feb 4, 2026)
Part 3: (46),(48) are possible only
in three cells c3,e3,e4, but they
can't be true at c3.e3 because (12)
would have no place. So one of
them must be true at e4, destroying
the path from 08 to 13 that takes
that cell. So,
6.(12)c3!! and 11 placements follow.
After these moves we get
28 27 26
,-----------------------------,
| __ 08 __ __ __ 25 __ | 7
| __ __ __ __ __ __ __ | 6 ... 09
| __ *29 __ __ __ __ __ | 5 ... 5,10,18,43,45
|*30 *11 04 49 *46 ww ww | 4 ... 42,17
|*31 *03 *12 47 *48 *41 16 | 3
| 02 *32 35 *13 *37 *15 *40 | 2
| 01 33 *34 *36 14 *38 *39 | 1
'-----------------------------'
a b c d e f g JCO#9
How to make progress from here ?
Update 6 (Feb 5, 2026)
(10)c5 will result in no digits
possible for cells a7,a8,a9. So,
19.(10)a5!! 20.(09)a6! with 6 additional placements.
We arrive at
,-----------------------------,
|*07 08 __ __ __ 25 __ | 7
|*09 *06 *28 __ *26 __ __ | 6 ... 44,19
|*10 *29 *05 *27 zz zz zz | 5 ... 18,43,45 locked
|*30 *11 04 49 *46 ww ww | 4 ... 42,17 locked
|*31 *03 *12 47 *48 *41 16 | 3
| 02 *32 35 *13 *37 *15 *40 | 2
| 01 33 *34 *36 14 *38 *39 | 1
'-----------------------------'
a b c d e f g JCO#9
[17,42],[18,43,45], {44,19},20,21,22,23,24
How to finish this ?
Final update (Feb 6, 2026)
One way to solve the puzzle is to notice that
18 must go to e5:
27.(18)e5!!
Otherwise, (19)g6, (20)g7, (21)f6 and the path
to 24 would go through e7, leaving no way to
reach back to 25.
After that move, only singles remain.////
It is usual that writing all these steps takes a lot
more time than actually solving the puzzle
with (actual) pencil and paper. In comparison
to Sudoku, we do not assign candidates to cells.
Notation in the sides of the board are very helpful
to remind us of the constraints.
Solving Hidoku with candidates for each cell is possible,
but it will make the solving a lot less appealing as a human
experience.