
Welcome!
This is part of JCOWebsite and contains all the proposed...
The following 5x5 Latin Squares Puzzle (generated with SudokuExplainer)
is rated SER = 8.3, and can be solved (manually) in four main steps.
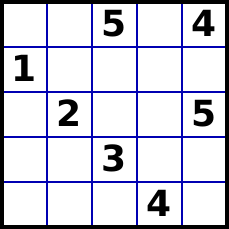
(image created using SudokuExplainer)
First write all candidates in each cell.
+-------------------------+
| 23 13 5 123 4 | 5
| 1 345 24 235 23 | 4
| 34 2 14 13 5 | 3
| 245 145 3 125 12 | 2
| 235 135 12 4 123 | 1
+-------------------------+
a b c d e Latin squares
+-------------------------+
| 23 13 5 123 4 | 5
| 1 345 24 25-3 23 | 4
| 34 2 14 13 5 | 3
| 245 145 3 125 12 | 2
| 235 135 12 4 123 | 1
+-------------------------+
a b c d e Latin squares
Step 1: We can eliminate (3)d4 using a sequence of bivalued cells.
Step 2: the harder part! (the reason for that SE rating).
,---------------------,
| 23 13 5 123 4 | 5
| 1 345 24 5-2 23 | 4
| 34 2 14 13 5 | 3
| 245 145 3 125 12 | 2
| 235 135 12 4 123 | 1
'---------------------'
a b c d e Latin squares
The suggestion is to study carefully the grid (above)
and try to find a way to show that 2 is false at that same cell d4.
If Step 2 is done, the puzzle can be solved in two more moves.
For step 3, the configuration is:
,-------------------------,
| 23 13 5 123 4 | 5
| 1 34 24 5 23 | 4
| 34 2 14 13 5 | 3
| 45 45 3 2-1 12 | 2
| 235 135 12 4 123 | 1
'-------------------------'
a b c d e Latin squares
One can eliminate (1) d2, using a simple chain wih 4 strong links.
For the last move, there is a pretty, simple idea! (see configuration below)
,---------------------,
| 2 13 5 13 4 |5
| 1 34 24 5 23 |4
| 34 2 14 13 5 |3
| 45 45 3 2 1 |2
| 35 135 12 4 23 |1 Latin squares
'---------------------'
a b c d e
I propose the following (interesting!) 6x6 Latin Squares Puzzle
that can be solved (manually) in five main steps.
(puzzle and image generated with SudokuExplainer)
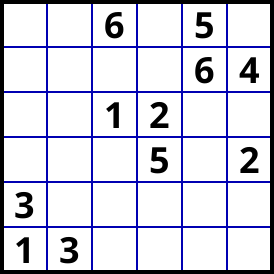
After no basics, the configuration is as follows.
+-------------------------------------+
| 24 124 6 134 5 13 | 6
| 25 125 235 13 6 4 | 5
| 456 456 1 2 34 356 | 4
| 46 146 34 5 134 2 | 3
| 3 12456 245 146 124 156 | 2
| 1 3 245 46 24 56 | 1
+-------------------------------------+ LS
a b c d e f
Update (March 18, 2025)
+-------------------------------------+
| 24 124 6 134 5 13 | 6
| 25 125 235 13 6 4 | 5
| 456 456 1 2 34 356 | 4
| 46 146 34 5 134 2 | 3
| 3 12456 245 46-1 124 156 | 2
| 1 3 245 46 24 56 | 1
+-------------------------------------+ LS
a b c d e f
For Step 1, there is an M-wing that eliminates (1)d2,
that creates a Naked Pair (46)d1.d2, that gives another
NP(13)d6.f6.
---
+-------------------------------------+
| 24 24 6 13 5 13 | 6
| 25 125 235 13 6 4 | 5
| 456 456 1 2 34 356 | 4
| 46 146 34 5 13-4 2 | 3
| 3 12456 245 46 124 156 | 2
| 1 3 245 46 24 56 | 1
+-------------------------------------+ LS
a b c d e f
For Step 2, a five strong linked chain shows that (4)e3 is false.
The ALS (124)e1.e2 has a role in this chain.
---
+-------------------------------------+
| 24 24 6 13 5 13 | 6
| 25 125 235 13 6 4 | 5
| 456* 456* 1 2 34 36-5 | 4
| 46* 146* 34 5 13 2 | 3
| 3 12456 245 46 124 156 | 2
| 1 3 245 46 24 56 | 1
+-------------------------------------+ LS
a b c d e f
Step 3 is nice and simple: a chain using the guardians of the
UR(46)a3,a4,b3,b4 proves that (5)f4 is false.
---
+-------------------------------------+
| 24 24 6 13 5 13 | 6
| 25 125 235 13 6 4 | 5
| 456 456 1 2 34 36 | 4
| 46 146 34 5 13 2 | 3
| 3 12456 245 46 124 156 | 2
| 1 3 245 46 24 56 | 1
+-------------------------------------+ LS
a b c d e f
How to proceed from here ?
Update (March 21, 2025)
For Step 4, we can remove (6)a4 using and AHS M-wing or an ALS W-wing.
This gives only one placement (+6) a3, but now b3 is a bivalued cell, and
we can finish the puzzle with a pretty Y-wing with transport,
eliminating (4)b4, (4)b6, and solving the puzzle with singles.
This 6x6 Latin Squares Puzzle ("spiral") is solvable in just one step. Can you find it ?
(puzzle and image generated with SudokuExplainer)
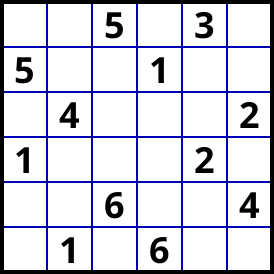
After basics (3 placements), the configuration is as follows.
+------------------------------+
| 46-2 26 5 24 3 1 | 6
| 5 236 234 1 46 36 | 5
| 36 4 1 35 56 2 | 4
| 1 356 34 345 2 356| 3
| 23 235 6 35-2 1 4 | 2
| 234 1 234 6 45 35 | 1
+------------------------------+
a b c d e f
The key is to remove (2)d2. Using a chain in 'spiral' (hence the name), we
actually get -2 a6, -2 d2, leaving only singles to the end.
("small space crowded with birds!")
I propose the following (tough!) Latin Squares Puzzle (SE = 8.3)
solvable in a couple steps (after basics).
(generated with SudokuExplainer)
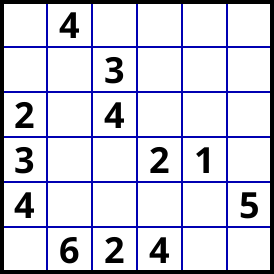
After basics moves, one should get the following configuration:
+-------------------------------+
| 16 4 5 136 236 1236 | 6
| 156 12 3 156 4 126 | 5
| 2 13 4 1356 356 136 | 4
| 3 5 6 2 1 4 | 3
| 4 23 1 36 236 5 | 2
| 15 6 2 4 35 13 | 1
+-------------------------------+
a b c d e f
Update 1: Jun 1, 2025
The first step was the hardest for me.
It took some time staring at the board to find
a (pretty) almost W-wing that eliminates (6)f6.
+-------------------------------+
| 16 4 5 136 236 123-6| 6
| 156 12 3 156 4 126 | 5
| 2 13 4 1356 356 136 | 4
| 3 5 6 2 1 4 | 3
| 4 23 1 36 236 5 | 2
| 15 6 2 4 35 13 | 1
+-------------------------------+
a b c d e f
Update 2: Jun 03, 2025
The almost w-wing already mentioned has main cells at
a6, a1,f1,f4 with (3)f4 as the spoiler.
The elimination of (6)f6 creates the strong link (6)f4=(6)f6
+-------------------------------+
| 16 4 5 136 236 123 | 6
| 156 12 3 156 4 (6)12 | 5
| 2 13 4 1356 356 (6)3-1| 4
| 3 5 6 2 1 4 | 3
| 4 23 1 36 236 5 | 2
| 15 6 2 4 35 13 | 1
+-------------------------------+
a b c d e f
that can be used to eliminate (1)f4 [using an L3-wing].
Final Update: Jun 4, 2025
From the second move, we have the bivalue cell (36)f4 that
can be used for a W-wing. There is another wing for move 4,
that eliminates (6)e4 giving the first placement: +6 f4.
This leads to
+----------------------------+
| 16 4 5 136 26 123 | 6
| 56 12 3 56 4 12 | 5
| 2 13 4 135 35 6 | 4
| 3 5 6 2 1 4 | 3
| 4 23 1 36 26 5 | 2
| 15 6 2 4 35 13 | 1
+----------------------------+
a b c d e f
Now, one has to find one last wing to finish this puzzle with singles.
I propose the following (also tough!) Latin Squares Puzzle (SE = 8.3)
solvable in few more challenging steps (after basics).
(generated with SudokuExplainer)
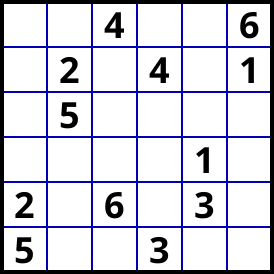
After a naked pair elimination, one should get the following configuration:
+-------------------------------+
| 13 13 4 25 25 6 | 6
| 36 2 35 4 56 1 | 5
| 1346 5 123 126 246 234 | 4
| 346 346 235 256 1 2345 | 3
| 2 14 6 15 3 45 | 2
| 5 146 12 3 246 24 | 1
+-------------------------------+
a b c d e f
Quite different solving experience in comparison to puzzle #51!
(no sequence of wings and harder first step).
Update (June 6, 2025)
I have solved this puzzle twice and in both solutions the
first step is complex !
Solution 1 has only 2 steps and explores the BV cells (13)a6, (13)b6,
and the strong links (1)a4=(1)a6, (3)b3=(3)b6 to show that (1)a4 is false.
After that elimination (involving a very complex move), we get two placements and
+-------------------------------+
| 1 3 4 25 25 6 | 6
| 36 2 35 4 56 1 | 5
| 346 5 123 126 246 234 | 4
| 346 46 235 256 1 2345 | 3
| 2 14 6 15 3 45 | 2
| 5 146 12 3 246 24 | 1
+-------------------------------+
a b c d e f
Now, there is a way finish this puzzle in one step.
Update (Jun 7, 2025)
The finishing move eliminates (3)a3 with a nice chain starting at
(4)a3 = (4)a4 - (4)e4 etc.
A second way to solve this puzzle starts with the idea of
exploring the weakness in the second row to get the elimination
(-5)d2 [and 3 placements] using a move still complex, but easier
the in solution 1.
After that, one gets the following configuration
+--------------------------------+
| 13 13 4 25 25 6 | 6
| 36 2 35 4 56 1 | 5
| 1346 5 123 26 246 234 | 4
| 346 36 235 256 1 234 | 3
| 2 4 6 1 3 5 | 2
| 5 16 12 3 246 24 | 1
+--------------------------------+
a b c d e f
Now, the puzzle can be solved at least with two simple chains.
Final Update (Jun 8, 2025)
For solution 1, one can see the first move as
+---------------------------------+
|(13) 13 4 25 25 6 | 6
|(3)6 2 (3)5 4 56 1 | 5
| 346-1 5 (13)2 [12]6 246 234 | 4
| 346 346 235 256 1 2345 | 3
| 2 14 6 15 3 45 | 2
| 5 146 12 3 246 24 | 1
+---------------------------------+
a b c d e f
'almost' W-wing (1=3)c4 - (3)c5 = (3)a5 - (3=1)a6
but there is the spoiler (2)c4, that we need to address.
If there is no (6)d4, then (2)c4 - (2=1)d4 also eliminates (1)a4.
So, the spoiler now is (6)d4. We can go down (to d3):
(6)d4 - (6)d3 = (6-4)a3 = (4)a4
that also eliminates (1)a4.
but we have the third spoiler (6)b3 and this is the
last one: (6)b3 - (3)b3 = (3)b6 - (3=1)a6
So, this is the very complex move that shows that (1)a4
can be removed. It all started with that 'almost' W-wing.
The configuration after this is:
+--------------------------------+
| 1 3 4 25 25 6 | 6
|(3)6 2 (35) 4 56 1 | 5
|(4)36 5 123 126 (4)26 234 | 4
|(4)6-3 46 (5)23 256 1 (5)234| 3
| 2 (14) 6 15 3 (45) | 2
| 5 (146) 12 3 (46)2 24 | 1
+--------------------------------+
a b c d e f
Now (4)a4 = a5 - e5 = (46-1)e1.b1 = (14-5)b2.f2 = (5)f3 - c3 = (5-3)c5 = (3)a5
eliminates (3) a3, producing a naked pair (46)a3.b3 that eliminates (6) d3.
After this the puzzle is solved easily with singles. ///
I have solved today the following Latin Squares Puzzle (SE = 7.1).
My solution has two steps (after basics).
(generated with SudokuExplainer)
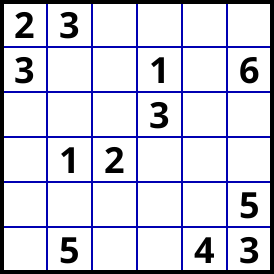
After basics
+-------------------------------+
| 2 3 456 456 56 1 |
| 3 24 45 1 25 6 |
| 1456 46 1456 3 156 2 |
| 56 1 2 56 3 4 |
| 146 246 3 46 126 5 |
| 16 5 16 2 4 3 |
+-------------------------------+LS
Update (Sept 21, 2025)
+-------------------------------+
| 2 3 456 456 56 1 | 6
| 3 24 5-4 1 25 6 | 5
| 1456 46 1456 3 156 2 | 4
| 56 1 2 56 3 4 | 3
| 146 246 3 46 126 5 | 2
| 16 5 16 2 4 3 | 1
+-------------------------------+LS
a b c d e f
A chain with 7 strong links implies that (4)c5 is false.
This elimination allows simplifications:
+-------------------------+
| 2 3 46 456 56 1 |
| 3 4 5 1 2 6 |
| 145 6 14 3 15 2 |
| 56 1 2 56 3 4 |
| 146 2 3 46 16 5 |
| 16 5 16 2 4 3 |
+-------------------------+LS
How to finish this puzzle ?
Update (Sept 24, 2025)
+------------------------+
| 2 3 46 456 56 1 |
| 3 4 5 1 2 6 |
| 145 6 14 3 15 2 |
| 56 1 2 56 3 4 |
| 146 2 3 4-6 16 5 |
| 16 5 16 2 4 3 |
+------------------------+LS
a b c d e f
M-wing eliminates (6)d2 solving the puzzle.