
Welcome!
This is part of JCOWebsite and contains all the proposed...
In the game called Slitherlink, can you show all the details
proving that the following configuration is impossible ?
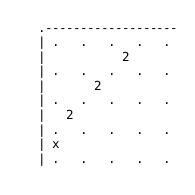
My solution has a trivial initial observation, an easy Case 1 and Case 2 divided in two sub-cases)
We analyze the possible outcomes from this configuration but can already discard all configurations
in which the lower "2"-cell has vertical lines, or horizontal lines, in both edges.
Also, this configuration
.-------------------
| . . . . .
| 2
| . . . . .
| 2
| .___. . . .
| | 2
|A. . . . .
| x
| . . . . .
and this
.-------------------
| . . . . .
| 2
| . . . . .
| 2
| . . . . .
| 2 |
|A.___. . . .
| x
| . . . . .
are clearly impossible (dead end at corner A).
Part 2
Case 1:
.-------------------
| . . . . .
| 2
| . . . . .
| 2
| .___. . . .
| 2 |
| . . . . .
| x
| . . . . .
Now the following is forced
.-------------------
| . .___.___. .
| x 2 |
| . .___. x . .
| | x 2 |
| .___. x . . .
| 2 |
| . . . . .
| x
| . . . . .
and this leads to an impossibility in the cell at the corner, reached
by three lines.
Part 3
Case 2:
.-------------------
| . . . . .
| 2
| . . . . .
| 2
| . . . . .
| | 2
| .___. . . .
| x
| . . . . .
The following is a forced move
.-------------------
| . . . . .
| 2
| . .B . . .
| | 2
| . x .A . . .
| | 2 x
| .___. . . .
| x
| . . . . .
Part 3.1
Case 2.1: If a vertical line exists at AB, it forces
.-------------------
| . . . . .
| | 2
| .C . . . .
| | | 2
| . x .___.D . .
| | 2 x
| .___. . . .
| x
| . . . . .
and any continuation for the line meeting
corner C will create a loop (impossible).
Part 3.2
Case 2.2: the other possibility is to have the edge AB blocked, and then the bottom edge
AD of the "2"-cell in the middle needs to be blocked too, forcing the following
configuration to be reached.
.-------------------
| . .___.___. .
| x 2 |
| . .___. x . .
| | x 2 |
| . x . x . . .
| | 2 x
| .___. . . .
| x
| . . . . .
Now, we have an impossible situation
in the cell at the corner, reached by three
lines.
(Using symmetry, the proven result establishes a well-known slitherlink pattern)
The following Jigsaw Sudoku Layout is invalid. Why ?
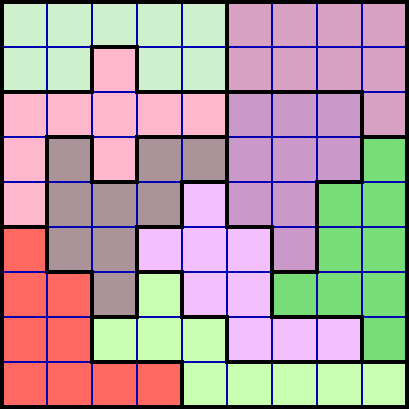
(image created using SudokuExplainer)
A Jigsaw Sudoku Layout is invalid if no Latin Squares exist for that Layouts.
Can you find a short, yet complete, explanation (no computations involved) ?
To my knowledge this question was first posed, and subsequently pursued, by Mathimagics.
Consider the following puzzle proposed by tarek at the NSPF in 2019.
See the hints for the grid after basics and NSPF link on ALP/ALT.
There is an Almost Locked Pair (ALP) that solves the puzzle with basics.
Part 1: Find the ALP and explain its logic in words (explanation given later at the hint section).
Part 2: Find an almost locked triple (ALT) that solves this puzzle (ste), and (the key part !)
find an explanation along the lines of the one given for Part 1.
Hope it will be fun, as it was for me some years ago.
link on ALP/ALT.
,-----------------------------------------------------------------------, | 137 579 8 | 2356 1367 257 | 134 12579 123457 | | 137 579 2 | 8 4 57 | 136 15679 1357 | | 6 4 135 | 235 137 9 | 13 1257 8 | |----------------------+----------------------+-------------------------| | 8 3 9 | 4 5 6 | 2 17 17 | | 2 1 4 | 7 9 8 | 5 3 6 | | 5 6 7 | 1 2 3 | 8 4 9 | |----------------------+----------------------+-------------------------| | 134 2 1356 | 9 367 457 | 1346 8 1345 | | 347 57 356 | 2356 8 1 | 9 256 2345 | | 9 8 1356 | 2356 36 245 | 7 1256 12345 | '-----------------------------------------------------------------------'
Update (Feb 9, 2026)
,-----------------------------------------------------------------------,
9 | 137 579 8 | 2356 1367 257 | 4-13 2579-1 123457 |
8 |(13)-7 579 2 | 8 4 57 |(13)6 (1)5679 (13)57 |
7 | 6 4 135 | 235 137 9 |(13) 257-1 8 |
|----------------------+----------------------+-------------------------|
6 | 8 3 9 | 4 5 6 | 2 17 17 |
5 | 2 1 4 | 7 9 8 | 5 3 6 |
4 | 5 6 7 | 1 2 3 | 8 4 9 |
|----------------------+----------------------+-------------------------|
3 | 134 2 1356 | 9 367 457 | 1346 8 1345 |
2 | 347 57 356 | 2356 8 1 | 9 256 2345 |
1 | 9 8 1356 | 2356 36 245 | 7 1256 12345 |
'-----------------------------------------------------------------------'
a b c d e f g h i
Almost locked pair (13)A,B,C where A=g8.h8.i8, B = g7, C = a8.
Let {a,b} be {1, 3}. If "a" is false at C, then (strong link) it must be true
at A, and the other digit "b" must be true at B. This explains the eliminations
at the top left box. The other elimination comes from the fact that we cannot
have a,b both out of C, because (strong link) they would be forced to be at A,
leaving (due to the weak link) the cell B empty.
So, the way to find this pattern directly [I often find it as a Loop] can be
to look at a bivalued cell and a mini-row (column) with those two digits and
see if it is strongly linked [in the Row (Column)] to a cell containing those
digits among its digits. This pattern appears a lot more than the ALT [Part 2].
Update (Feb 10, 2026)
I often find such move (ALP) in the form
Loop (1-3)a8 = (3)g8.i8 - (3=1)g7 - (1)g8.h8.i8 = (1-3)a8 => -13 g9.i9, -1 h7.h9, -7 a8; lclste
Regarding Part 2, the almost locked triple instead of the ALP solves the puzzle with singles
as follows:
.-----------------------------------------------------------------------------.
| 137 579 8 | 36-25 136-7 [257] | 134 12579 123457 |
| 137 579 2 | 8 4 [57] | 136 15679 1357 |
| 6 4 [5]-13 |(25)3 13(7) 9 | 13 (257)-1 8 |
|-------------------------+-------------------------+-------------------------|
| 8 3 9 | 4 5 6 | 2 17 17 |
| 2 1 4 | 7 9 8 | 5 3 6 |
| 5 6 7 | 1 2 3 | 8 4 9 |
|-------------------------+-------------------------+-------------------------|
| 134 2 1356 | 9 367 457 | 1346 8 1345 |
| 347 57 356 | 2356 8 1 | 9 256 2345 |
| 9 8 1356 | 2356 36 245 | 7 1256 12345 |
'-----------------------------------------------------------------------------'
ALT (257) r3c45,r3c38,r12c6 => -25 r1c4, -7 r1c5, -13 r3c3, -1 r3c8; ste
. What would be the Loop associated to this move ?
. Which other reasoning can explain the move (outside the scope of the next item) ?
. The key reason for this problem 3 is to ask for an explanation for this move
along the lines given for ALP.
Problems are seen here as open-ended questions (not being mere exercises).
For this part no further comments will be made.