
Welcome!
This is part of JCOWebsite and contains all the proposed...
I propose the following interesting 6x6 Slitherlink puzzle.
(solving it means to write a detailed solution of each step)
(From Simon Tatham's Portable Puzzle Collection)

This puzzle (rated hard) can be solved (manually) in 7 steps using well-known patterns.
My first step (basics) ends here:
. x . . . .___. .
x 3 2 2
.___. . . . . .
| 3 2 |
. . . . . . .
3 | 2 1 2
. .___. x . . . .
2 x 0 x
. .___. x .___. . .
3 | | 3 3
. . . . . . .
2 2
. . . . . . .
Step 2:
. x . . . .___. .
x => | 3 2 2
.___. . . . . .
| 3 2 |
. . . . . . .
3 | 2 1 2
. .___. x . . . .
2 x 0 x
. .___. x .___. . .
3 | | 3 3
. . . . . . .
2 2
. . . . . . .
The justification for step 2 is:
. x .===.===. .___. .
x ] 3 ] 2 2
.___. x .===. . . .
| 3 | 2 |
.===. x . . . . .
x ] 3 | 2 1 2
? x .___. x . . . .
] 2 x x 0 x
.===.___. x .___. .___.
3 | | 3 3
. . . . . . .
2 2
. . . . . . .
and line ending at (?) has no place to go.
The idea of writing out a detailed solution path is to break the solution into n parts
where each part is a well-identified pattern that can be used in other puzzles
(each hopefully having a short and elegant proof).
An example of this is the pattern in the lower-right corner.
. . .___. . . | . . .___. .___. |
| 3 3 | | 3 | 3 |
. . . . . . | . . . . . . |
2 | => 2 x | |
. . . . . . | . . . .___.___. |
----------------------' ----------------------'
Proof: either possible configuration for the 3-cell in
the left gets into the left upper corner of 2, and so
it must leave 2 at the lower right corner, implying that
horizontal line at the corner, that can only go up.
Now that last line arrived at the lower right corner
of the 3-cell on the right, and so the two edges that
do not contain that corner must be true.
The "x" avoids a small 2 cells-loop contaning the "3"
and additional horizontal line at the bottom follows from this.
The final configuration is the following
. .___. .___.___.___.
| | 3 | 2 2 |
.___. .___. .___. .
| 3 2 | | |
.___.___. .___. .___.
3 | 2 | 1 2
.___.___. .___.___.___.
| 2 0 |
. .___. .___. .___.
| | 3 | | 3 | | 3
. . . . . .___.
| | 2 | | | 2 |
.___. .___. .___.___.
After some hard work, I solved (manually) the following tough Slitherlink puzzle.
I hope that, by proposing it here, someone will have as much fun as I had solving it.
(From Simon Tatham's Portable Puzzle Collection)

x
1 3
_ _
3 1
x
helps to develop the upper-right part of this puzzle
(see Para's puzzle site)
.-------------------------------.
| . . . x . x .___.___.___. |
| 1 x | 2 x x | |
| . . . .___. x .___.___. |
| 1 x 1 | 3 x 1 x |
| . . . .___. x .___. x . |
| 3 | 1 x 2 | x |
| . . . . . x . x . . | |
| 3 2 x 2 | 2
| . . . . .___. x . . | |
| 1 x 1 3 | 2 3 | |
| . . x . x . . . . . |
| x 1 | 3 2 x |
| . . . x .___. . . . |
| | 3 1 x 2 |
| .___. . . . . . . |
'-------------------------------'
Now after analyzing the right side of the puzzle,
two simple inferences lead to substantial progress:
.-------------------------------.
| . . . x . x .___.___.___. |
| 1 x | 2 x x | | 7
| . . . .___. x .___.___. |
| 1 x 1 | 3 x 1 x | 6
| . . . .___. x .___. x . |
| x x 3 | 1 x 2 | x | 5
| . x .___. x .___. x . x . x . |
| | 3 | 2 x x | 2 x | 4
| . . .___. x .___. x .___. |
| 1 x 1 x | 3 | 2 x 3 | | 3
| . . x . x .___. x .___.___. |
| | x 1 | 3 x x 2 x x | 2
| .___. . x .___.___.___.___. |
| | 3 x x 1 x x 2 x | | 1
| .___.___.___.___.___.___.___. |
'-------------------------------'
a b c d e f g
Now looking at (1)c6, one finds the final inference
to finish the puzzle.
Final configuration:
.-------------------------------.
| .___.___. . .___.___.___. |
| | | 1 | 2 | |
| . .___. .___. .___.___. |
| | | 1 | 1 | 3 1 |
| . .___. .___. .___. . |
| | | 3 | 1 2 | |
| . .___. .___. . . . |
| | | 3 | 2 | 2 |
| . .___.___. .___. .___. |
| | 1 1 | 3 | 2 3 | |
| .___. . .___. .___.___. |
| | 1 | 3 2 |
| .___. . .___.___.___.___. |
| | 3 1 2 | |
| .___.___.___.___.___.___.___. |
'-------------------------------'
The following tough Slitherlink puzzle has two blank rows and almost no standard patterns.
It was fun to find a way to solve it in a few steps.
(Interesting puzzle from the site www.themissingdocs.net)

Update (Sept 20, 2025)
Grouping easy moves, this puzzle is solvable in 5 main steps.
After basic moves (Step 1):
.-------------------------------.
| . . . . . . . . |
| 0 1 | 7
| . . . . . . . . |
| 0 1 2 0 | 6
| . . . . . . . . |
| | 5
| . . . . . .___.___. |
| 1 1 1 | | 4
| . . . .___. . . . |
| 2 3 | 3 0 1 | | 3
| . . . . .___. . . |
| | | | 2
| . . . . . .___. . |
| | 3 2 0 2 | | | 1
| .___. . . . . .___. |
'-------------------------------'
a b c d e f g
Now (Step 2),
. We must have x at the right of (1)e7.
. We must have x at the top of (1)c6.
. We must have x at the top of (1)a4.
.-------------------------------.
| . . . . . . . . |
| 0 1 x | 7
| . . . x . . . . . |
| 0 1 2 0 | 6
| . . . . . . . . |
| | 5
| . x . . . . .___.___. |
| 1 1 1 | | 4
| . . . .___. . . . |
| 2 3 | 3 0 1 | | 3
| . . . . .___. . . |
| | | | 2
| . . . . . .___. . |
| | 3 2 0 2 | | | 1
| .___. . . . . .___. |
'-------------------------------'
a b c d e f g
The next moves seem to require more analysis!
Update (Sept 22, 2025)
Step 3. It is impossible to have x at the left of (1)a4,
because it forces (3l)b3 or (3t)b3, so (3b)b3,(3r)b3,
and (3l)b3 is impossible (due to (2)a3).
.-------------------------------.
| . . . . . . . . |
| 0 1 x | 7
| . . . x . . . . . |
| 0 1 2 0 | 6
| . . . . . . . . |
| | 5
| . x . . . . .___.___. |
|?x 1 1 1 | | 4
| . . . .___. . . . |
| 2 3 | | 3 0 1 | | 3
| . .___. . .___. . . |
| | | | 2
| . . . . . .___. . |
| | 3 2 0 2 | | | 1
| .___. . . . . .___. |
'-------------------------------'
a b c d e f g
So (3t)b3, forcing (2t)a3, (2l)a3, ( l)a2,
(3r)a1 and we get an undesirable loop,
or not place for (3b)b3 to go.
.-------------------------------.
| . . . . . . . . |
| 0 1 x | 7
| . . . x . . . . . |
| 0 1 2 0 | 6
| . . . . . . . . |
| | 5
| . x . . . . .___.___. |
|?x 1 1 1 | | 4
| .___.___. .___. . . . |
| | 2 3 | | 3 0 1 | | 3
| . .___. . .___. . . |
| | | | | 2
| . . . . . .___. . |
| | 3 | 2 0 2 | | | 1
| .___. . . . . .___. |
'-------------------------------'
a b c d e f g
So, 16. (1l)a4!!
.-------------------------------.
| . . . . . . . . |
| 0 1 x | 7
| . . . x . . . . . |
| 0 1 2 0 | 6
| . . . . . . . . |
| | 5
| . x . . . . .___.___. |
| | 1 1 1 | | 4
| . . . .___. . . . |
| 2 3 | 3 0 1 | | 3
| . . . . .___. . . |
| | | | 2
| . . . . . .___. . |
| | 3 2 0 2 | | | 1
| .___. . . . . .___. |
'-------------------------------'
a b c d e f g
Step 4. We work on the consequences of (1l) a4:
.-------------------------------.
| . . . . . . . . |
| 0 1 x | 7
| . . . x . . . . . |
| 0 1 2 0 | 6
| .___. . . . . . . |
| | | | 5
| . x .___. . . .___.___. |
| | 1 1 1 | | 4
| . .___. .___. . . . |
| | 2 | 3 | 3 0 1 | | 3
| . . . . .___. . . |
| | | | | 2
| . . . . . .___. . |
| | 3 | 2 0 2 | | | 1
| .___. . . . . .___. |
'-------------------------------'
a b c d e f g
How to continue ?
Update (Sept 24, 2025)
A line at the top of (2)b2 leads
quickly to a situation where a line
has not place to go. So, there must
be a line at the right of cell a2.
This inference leads to a sequence
of forced moves and the configuration
.-------------------------------.
| . . . . . . . . |
| 0 1 x | 7
| . . . x . . . . . |
| 0 1 2 0 | 6
| .___. . . . . . . |
| | | | 5
| . .___. . .___.___.___. |
| | 1 1 1 | | 4
| . .___. .___. . . . |
| | 2 | 3 | | 3 | 0 1 | | 3
| . . . . .___. . . |
| | | | | | | | 2
| . . . . . .___. . |
| | 3 | 2 | | 0 2 | | | 1
| .___. .___. . . .___. |
'-------------------------------'
a b c d e f g
How to finish this puzzle ?
(Update Sept 27, 2025)
Now we notice that (2)e6 must
have a line coming in the lower
left corner and leaving in the
top right corner, since all other
possibilities leave a line without
place to go. So, there must be
a line at the bottom of ( )f7,
and at the right and top too.
.-------------------------------.
| . . . . . .___. . |
| 0 1 x | | 7
| . . . x . . .___. . |
| 0 1 2 0 | 6
| .___. . . . . . . |
| | | | 5
| . .___. . .___.___.___. |
| | 1 1 1 | | 4
| . .___. .___. . . . |
| | 2 | 3 | | 3 | 0 1 | | 3
| . . . . .___. . . |
| | | | | | | | 2
| . . . . . .___. . |
| | 3 | 2 | | 0 2 | | | 1
| .___. .___. . . .___. |
'-------------------------------'
a b c d e f g
The rest is simple.
.-------------------------------.
| . . . .___.___.___. . |
| 0 | 1 | | 7
| . . . . . .___. . |
| 0 1 | 2 | 0 | 6
| .___. . . .___. . . |
| | | | | | 5
| . .___.___. .___.___.___. |
| | 1 1 1 | | 4
| . .___. .___. . . . |
| | 2 | 3 | | 3 | 0 1 | | 3
| . . . . .___. . . |
| | | | | | | | 2
| . . . . . .___. . |
| | 3 | 2 | | 0 2 | | | 1
| .___. .___. . . .___. |
'-------------------------------'
a b c d e f g
The following tough 7x7 Slitherlink is my first puzzle.
It was a lot of fun to create it full of patterns.
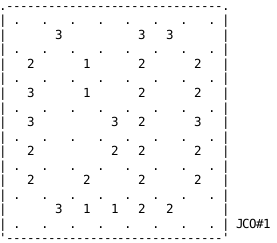
.-------------------------------.
| . . . .___. x .___. x . |
| | 3 | | 3 | 3 | x | 7
| . x . . . x .___. x . . |
| 2 1 x 2 x 2 | 6
| .___. . . .___. . . |
| 3 1 2 2 | | 5
| .___. x . . . . . . |
| 3 3 2 | 3 | 4
| .___. . . . . x .___. |
| 2 2 2 x 2 | 3
| . . . . . . . . |
| 2 2 2 2 | 2
| . . . x . . . . . |
| 3 | 1 x 1 2 2 | 1
| . .___. x . x . . . . |
'-------------------------------'
a b c d e f g JCO#1 (Slitherlink)
In the next 3 steps (not shown, but described), it is used twice the fact
that the number of lines in row 6 must be even.
Steps:
1) for the reason above, no line to the left of (2)g6;
2) a vertical line must exist at (2)a6 and, for the reason above,
no vertical line is true at (1)c6;
(3) next, the horizontal line at the top of (1)c5 leads to a quick contradiction.
After 3), it is easy to finish the puzzle.
Final configuration:
.-------------------------------.
| . .___. .___. .___. . |
| | 3 | | | 3 | 3 | |
| . . .___. .___. .___. |
| 2 | 1 2 2 | |
| .___. . .___.___. . . |
| | 3 1 | 2 | 2 | |
| .___. . .___. . .___. |
| 3 | 3 | 2 | | 3 |
| .___. . .___. . .___. |
| | 2 | 2 2 | 2 | |
| . . .___. .___. . . |
| | 2 | 2 | 2 2 | |
| .___. . . . . .___. |
| | 3 | 1 1 | 2 2 | |
| . .___. . .___.___. . |
'-------------------------------' JCO#1
I did not try to solve the puzzle without using that fact.
I have battled with a nice Slitherlink puzzle (hard) from Simon Tatham's collection.

Rules:
1. Connect adjacent dots with vertical or horizontal lines to make a single loop.
2. The numbers indicate how many lines surround it, while empty cells may be surrounded by any number of lines.
3. The loop never crosses itself and never branches off.
I have found a solution in 4 main steps: one can make good progress at the start,
using the two 3s at the corners, the sole "0" and that one cannot have
a line between 1 and 2 in column "g", etc. This start leads to
a long sequence of forced moves.
.-------------------------------.
| . . . . . .___.___. |
| 2 | 3 3 | | 7
| . . . . x .___. .___. |
| 1 2 1 x x | 6
| . . . . . . .___. |
| 2 2 1 3 | | 5
| . . . . . . x .___. |
| 2 | x | 4
| . . x . . . . x .___. |
| 3 | 1 x 1 1 x 0 x 2 | | 3
| .___. x . . . x . x . x . |
| x 1 | 1 x x 1 | | 2
| . . . .___. x .___. x . |
| | 3 2 2 x 2 | 3 | | | 1
| .___. . .___.___. .___. |
'-------------------------------'
a b c d e f g
The position above is still part 1 (with basic moves still available).
Later on, further analysis is needed to advance (see next).
.-------------------------------.
| . . . x .___. .___.___. |
| 2 | | 3 | 3 | | 7
| . . . . x .___. x .___. |
| 1 2 1 x x | x | 6
| . . . . . x . x .___. |
| | 2 2 1 x 3 | | 5
| . x . . . . . x .___. |
| | | 2 | x | 4
| . . x . . . . x .___. |
| | 3 | 1 x 1 1 x 0 x 2 | | 3
| .___. x . x . . x . x . x . |
| x x 1 x x | 1 x x 1 | | 2
| .___.___.___.___. x .___. x . |
| | 3 2 2 x 2 | 3 | | | 1
| .___.___.___.___.___. .___. |
'-------------------------------'
a b c d d f g
In the configuration above, (1r)c3 leads to a contradiction.
[(1r)c3 means a line to the right of the cell c3 (it has a 1)]
[The contradiction was: three lines arriving at (2)b5]
Now
.-------------------------------.
| . . . x .___. .___.___. |
| 2 | | 3 | 3 | | 7
| . . .___. x .___. x .___. |
| 1 2 x 1 x x | x | 6
| . . . .___. x . x .___. |
| | 2 2 | 1 x 3 | | 5
| . x . . . . x . x .___. |
| | | | 2 x | x | 4 already four vertical lines at line 4,
| . . x .___. . x . x .___. | so _
| | 3 | 1 x 1 x | 1 x 0 x 2 | | 3 |2
| .___. x . x . x . x . x . x . | and
| x x 1 x x | 1 x x 1 | | 2 2 |
| .___.___.___.___. x .___. x . | ___.
| | 3 2 2 x 2 | 3 | | | 1
| .___.___.___.___.___. .___. | are not possible for (2)d4 !
'-------------------------------'
a b c d e f g
Next, one can show that (2l)d4 and (2r)d4 true lead quickly to a contradiction.
So, (2b)d4 and (2t)d4 must be true [notation: l=left,r=right,t=top,b=bottom]
Now the puzzle is finished easily using once more that idea
of having an even number of lines in a row or column.
Final configuration:
.-------------------------------.
| .___.___. .___. .___.___. |
| | 2 | | | 3 | 3 | |
| . . .___. .___. .___. |
| | 1 2 1 | |
| . .___.___.___. . .___. |
| | 2 | 2 | 1 3 | |
| . . .___.___. . .___. |
| | | | 2 | |
| . . .___.___. . .___. |
| | 3 | 1 1 | 1 0 2 | |
| .___. . . . . . . |
| 1 | 1 1 | |
| .___.___.___.___. .___. . |
| | 3 2 2 2 | 3 | | |
| .___.___.___.___.___. .___. |
'-------------------------------'
This interesting Slitherlink puzzle has a tough start.
(puzzle from Simon Tatham's Collection)
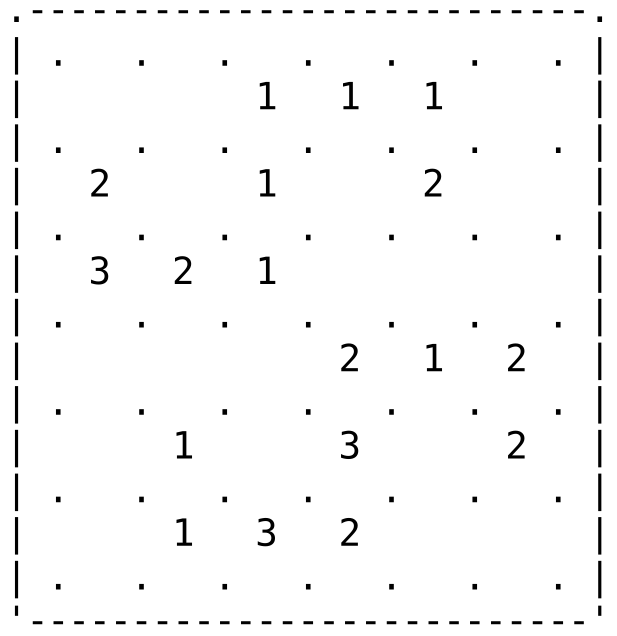
.---------------------------. | . . . . . . . | | 1 1 1 | | . . . . . . . | | 2 1 2 | | . . . . . . . | | 3 2 1 | | . . . . . . . | | 2 1 2 | | . . . . . . . | | 1 3 2 | | . . . . . . . | | 1 3 2 | | . . . . . . . | '---------------------------' Rules: 1. Connect adjacent dots with vertical or horizontal lines to make a single loop. 2. The numbers indicate how many lines surround it, while empty cells may be surrounded by any number of lines. 3. The loop never crosses itself and never branches off.
The following is a sketch of my solution in 3 steps:
Step 1:
.---------------------------. | . . . . . . . | | 1 x 1 x 1 | | . . . . . . . | | 2 1 2 | | . . . . . . . | | 3 2 1 | | . . . . . . . | | 2 x 1 2 | | . . . .___. x . . | | x x 1 3 | 2 | | . x . x . . . x . . | | x x 1 | 3 2 | | . x . x .___. . . . | '---------------------------'
Step 2 (4 parts):
to show that the line marked === below leads to contradiction. .---------------------------. | . . . . . . . | | 1 x 1 x 1 | | . . . . . . . | | 2 1 2 | | . . . . . . . | | 3 2 1 | | . . . . . . . | | 2 x 1 2 | | . .===. .___. x . . | | x x 1 x 3 | 2 | | . x . x . . . x . . | | x x 1 | 3 2 | | . x . x .___. . . . | '---------------------------'
Step 3:
to show that the line === shown below leads to contradiction. .---------------------------. | . . . . . . . | | 1 x 1 x 1 | | . . . x . . . . | | 2 1 x 2 | | . . . . . . . | | | 3 2 1 | | .___. . . . . . | | x x | 2 x 1 2 | | . x . x . x .___. x . . | | x x 1 | 3 | 2 | | . x . x . x .===. x . . | | x x 1 | 3 | 2 | | . x . x .___. x . . . | '---------------------------'
After this, the puzzle is solved quickly.
The final configuration is
.---------------------------. | .___.___.___.___.___.___. | | | 1 1 1 | | | .___.___. . . .___. | | 2 | 1 2 | | | .___.___. .___.___. . | | | 3 2 1 | | | .___.___. .___.___.___. | | | 2 1 2 | | | . . . .___. . . | | 1 | | 3 | 2 | | | . . . . . .___. | | 1 | 3 | 2 | | | | . . .___. .___. . | '---------------------------'
The following (tough) Slitherlink puzzle is my second puzzle.
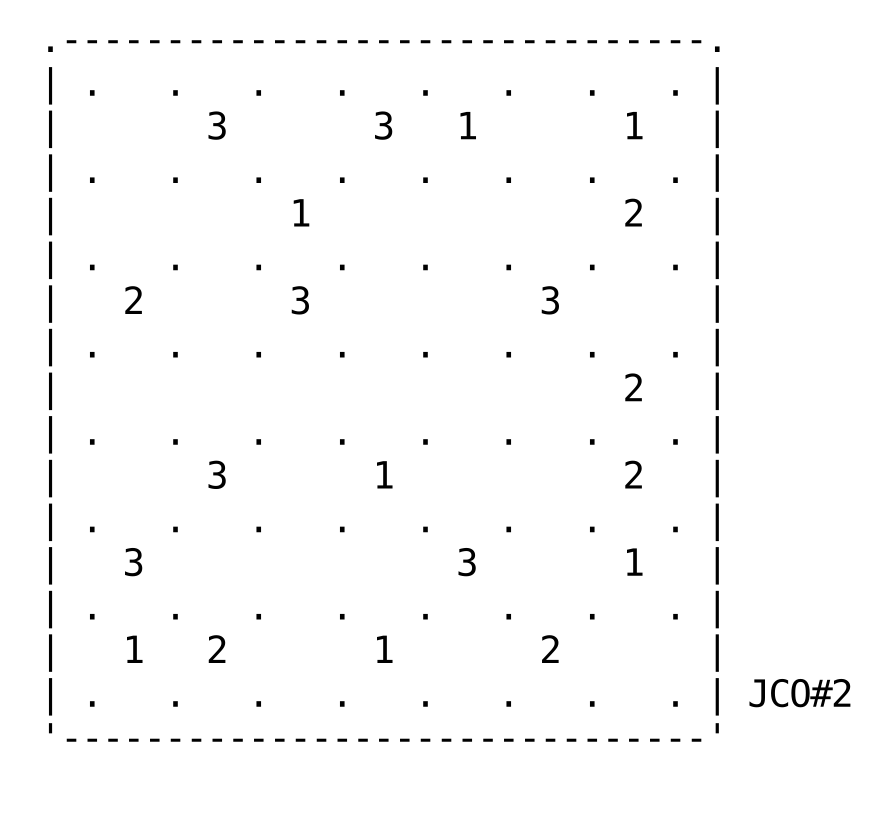
.-------------------------------.
| . . . . . . . . |
| 3 3 1 1 |
| . . . . . . . . |
| 1 2 |
| . . . . . . . . |
| 2 3 3 |
| . . . . . . . . |
| 2 |
| . . . . . . . . |
| 3 1 2 |
| . . . . . . . . |
| 3 3 1 |
| . . . . . . . . |
| 1 2 1 2 |
| . . . . . . . . | JCO#2
'-------------------------------'
Rules:
1. Connect adjacent dots with vertical or horizontal lines to make a single loop.
2. The numbers indicate how many lines surround it, while empty cells may be surrounded by any number of lines.
3. The loop never crosses itself and never branches off.
Basics moves lead to
.-------------------------------.
| . . . .___. x . x . x . |
| 3 3 | 1 x x 1 x | 7
| . . . . . x .___.___. | (only way!)
| x 1 | x 2 | | 6
| . .___. x . . x .___. x . |
| 2 | 3 | 3 | | | 5
| . . x .___. x . .___. x . |
| x x 2 | | 4
| . .___. x . x . . x .___. |
| x 3 | x 1 | | 2 x | 3
| .___. . . . x . x . x . |
| | 3 x x x | 3 | | 1 x | 2
| .___.___. x . x .___. x . . |
| 1 x 2 | x 1 x x 2 | | 1
| . . x .___.___.___.___. . |
'-------------------------------' JCO#2
a b c d e f g
Following this, two more inferences were needed to get
.-------------------------------.
| .___.___. .___. . . . |
| | 3 | | 3 | 1 1 |
| . .___. . . .___.___. |
| | | 1 | | | 2 | |
| . .___. . . .___. . |
| | 2 | 3 | | 3 | | |
| .___. .___. . .___. . |
| | | | 2 | |
| . .___. . . . .___. |
| 3 | 1 | | | 2 |
| .___.___. . . . . . |
| | 3 | 3 | | 1 |
| .___.___. . .___. . . |
| 1 2 | 1 2 | |
| . . .___.___.___.___. . | JCO#2
'-------------------------------'
I propose the following (interesting!) Slitherlink puzzle:
(From Simon Tatham's Portable Puzzle Collection)

Initial configuration in text format (and notation)
.---------------------------------------.
| . . . . . . . . . . |
| 3 2 3 | 9
| . . . . . . . . . . |
| 2 2 1 2 1 | 8
| . . . . . . . . . . |
| 3 2 3 3 | 7
| . . . . . . . . . . |
| 1 3 1 2 2 | 6
| . . . . . . . . . . |
| 1 2 3 | 5
| . . . . . . . . . . |
| 2 2 2 1 2 | 4
| . . . . . . . . . . |
| 1 | 3
| . . . . . . . . . . |
| 3 2 2 | 2
| . . . . . . . . . . |
| 3 2 3 2 2 2 3 | 1
| . . . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
Rules:
1. Connect adjacent dots with vertical or horizontal lines to make a single loop.
2. The numbers indicate how many lines surround it, while empty cells may be surrounded by any number of lines.
3. The loop never crosses itself and never branches off.
Notation: (3r)c6 means to place a line segment at the
right-edge of cell c6 (has a number 3 on it).
( b)b1 means to place a line segmento at the
bottom of the cell b1, which has no number in it.
(2xr)c1 means to place an 'x' at the right-edge of
cell c1, which has number 2 in it.
Update (Feb 23, 2025): for now, hints for Steps 1, 2
Step 1: patterns with 3s
.---------------------------------------. __
| . . . . .___.___.___.___.___. | 3|
| 3 2 3 | | 9 (3)i9 [corner] interacting with (1)h8: 1
| . . . . . .___.___.___.___. |
| 2 2 1 x 2 x 1 x x | 8
| . . . . . . .___. x .___. |
| 3 2 | 3 | 3 | | 7 3|3 at cells f7, i7
| . . . . . . . .___. . |
| 1 3 1 2 x 2 | | 6
| . . . . . . . . .___. |
| 1 2 3 | 5
| . . . . . . . . . . |
| 2 2 2 1 2 | 4
| . . . . . . . . . . |
| 1 x | 3
| . . . . .___. x . . . . |
| 3 | 2 2 | 2 3
| . . . . . . . . . . | 3 at cells d1, e2
| | 3 2 | 3 2 2 2 3 | | 1
| .___. . x .___. . . . .___. | two 3s at corners a1, i1
'---------------------------------------'
a b c d e f g h i
In Step 2, one can show that (2xr)f2 is false [leads quickly to contradiction].
So, (2r)f2. Now, progress can be made at cells h1, h5, g4.
The resulting configuration is
.---------------------------------------.
| . . . . .___.___.___.___.___. |
| 3 2 3 | | 9
| . . . . . .___.___.___.___. |
| 2 2 1 x 2 x 1 x x | 8
| . . . . . . .___. x .___. |
| 3 2 | 3 | 3 | | 7
| . . . . . . . x .___. . |
| 1 3 1 2 x x 2 | | 6
| . . . . . . . . .___. |
| 1 2 | 3 x | 5
| . . . . . . . x .___. . |
| 2 2 2 1 x | 2 x | 4
| . . . . . x . x .___. . . |
| 1 x x | 3
| . . . . .___. x .___. . . |
| 3 | 2 | 2 x | 2
| . . . . . . x . . .___. |
| | 3 2 | 3 2 2 2 x 3 | | 1
| .___. . x .___. . . .___.___. |
'---------------------------------------'
a b c d e f g h i
Update (Feb 25, 2025)
For step 3, one can investigate the consequences
of (3t)d1. That possibility gives a quick contradiction:
a line at (1b)a5 that can't go down, and so it does not
have a place to go. So, there is a line segment at (3r)d1
and that allows one to make progress:
.---------------------------------------.
| . . . . .___.___.___.___.___. |
| 3 2 3 | | 9
| . . . . . .___.___.___.___. |
| 2 2 x 1 2 x 1 x x | 8
| . . . . . x . .___. x .___. |
| 3 2 | 3 | 3 | | 7
| . . . . . . . x .___. . |
| 1 3 1 2 x x 2 | | 6
| . . . . . . .___. .___. |
| 1 2 | 3 | x | 5
| . . . . . . . x .___. . |
| 2 2 2 1 x | 2 x | 4
| . . . . . x . x .___.___.___. |
| 1 x x x | | 3
| . . . . x .___. x .___.___.___. |
| | 3 | 2 | 2 x | 2
| . . . . . . x .___.___.___. |
| | 3 2 | 3 | 2 | 2 x 2 x 3 | | 1
| .___. . x .___. x .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
Now, where does the line segment at (2l)g4 goes to?
For Step 4, one can show that ( r)f5 is false (also quick contradiction)
and explore the consequences of ( t)f4 being true.
.---------------------------------------.
| . . . . .___.___.___.___.___. |
| 3 2 3 | | 9
| . . . . . .___.___.___.___. |
| 2 2 x 1 2 x 1 x x | 8
| . . . . . x . .___. x .___. |
| 3 2 | 3 | 3 | | 7
| . . . . . . . x .___. . |
| 1 3 1 2 x x 2 | | 6
| . . . . . . .___. .___. |
| 1 2 x | 3 | x | 5
| . . . . . .___. x .___. . |
| 2 2 2 1 x | 2 x | 4
| . . . . . x . x .___.___.___. |
| 1 x x x | | 3
| . . . . x .___. x .___.___.___. |
| | 3 | 2 | 2 x | 2
| . . . . . . x .___.___.___. |
| | 3 2 | 3 | 2 | 2 x 2 x 3 | | 1
| .___. . x .___. x .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
For Step 5, one can show that if ( b)a2, then
(1)e4 would have no lines possible in all its edges!
So, (3r)a1 has a line and as a consequence:
.---------------------------------------.
| . . . . .___.___.___.___.___. |
| 3 2 3 | | 9
| . . . . . .___.___.___.___. |
| 2 2 x 1 2 x 1 x x | 8
| . . . . . x . .___. x .___. |
| 3 2 | 3 | 3 | | 7
| . . . . . . . x .___. . |
| 1 3 1 2 x x 2 | | 6
| . . . . . . .___. .___. |
| 1 2 x | 3 | x | 5
| . . . . . .___. x .___. . |
| 2 2 2 1 x | 2 x | 4
| . x . . . . x . x .___.___.___. |
| 1 x x x x | | 3
| . . . . x .___. x .___.___.___. |
| | x | 3 | 2 | 2 x | 2
| . . .___. x . . x .___.___.___. |
| | 3 | x 2 | 3 | 2 | 2 x 2 x 3 | | 1
| .___. x . x .___. x .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
(Update: Feb 26, 2025)
Step 6: (2r)a4 is impossible! (trouble to fulfill cell (2)a4).
Also from the pattern 2-2 in diagonal at f6, e7: (2l)e7, (2b)d8 must be true.
We obtain the following configuration:
.---------------------------------------.
| . . . . .___.___.___.___.___. |
| 3 2 3 | | 9
| . . . . . .___.___.___.___. |
| | 2 2 x 1 2 x 1 x x | 8
| . . . .___. x . .___. x .___. |
| | 3 | | 2 | 3 | 3 | | 7
| .___. x . . . . . x .___. . |
| x x 1 | 3 1 2 x x 2 | | 6
| . x . x .___. . . .___. .___. |
| x 1 x x 2 x | 3 | x | 5
| .___.___. x . . .___. x .___. . |
| | 2 x 2 | 2 1 x | 2 x | 4
| . x . x . . . x . x .___.___.___. |
| | 1 x x x x | | 3
| . x . . . x .___. x .___.___.___. |
| | x | 3 | 2 | 2 x | 2
| . x . .___. x . . x .___.___.___. |
| | 3 | x 2 | 3 | 2 | 2 x 2 x 3 | | 1
| .___. x . x .___. x .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
Step 7: This is a key step. If (2b)c4 is true, we violate uniqueness (why ?).
so we must have (2r)c4.
.---------------------------------------.
| . . . . .___.___.___.___.___. |
| 3 2 3 | | 9
| . . . . . .___.___.___.___. |
| | 2 2 x 1 2 x 1 x x | 8
| . . . .___. x . .___. x .___. |
| | 3 | | 2 | 3 | 3 | | 7
| .___. x . . . . . x .___. . |
| x x 1 | 3 1 2 x x 2 | | 6
| . x . x .___. . . .___. .___. |
| x 1 x x 2 x | 3 | x | 5
| .___.___. x . . .___. x .___. . |
| | 2 x 2 | 2 | 1 x | 2 x | 4
| . x . x . x . . x . x .___.___.___. |
| | 1 x | x x x | | 3
| . x . . . x .___. x .___.___.___. |
| | x | 3 | 2 | 2 x | 2
| . x . .___. x . . x .___.___.___. |
| | 3 | x 2 | 3 | 2 | 2 x 2 x 3 | | 1
| .___. x . x .___. x .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
Step 8: Another key step!
At the region with cells b2, b3, c2, c3,
we have three paths, so to avoid contradiction
we must have as true ( t)b1 and ( b)c3, ( r)c3,
like this
.---------------------------------------.
| . . . . .___.___.___.___.___. |
| 3 2 3 | | 9
| . . . . . .___.___.___.___. |
| | 2 2 x 1 2 x 1 x x | 8
| . . . .___. x . .___. x .___. |
| | 3 | | 2 | 3 | 3 | | 7
| .___. x . . . . . x .___. . |
| x x 1 | 3 1 2 x x 2 | | 6
| . x . x .___. . . .___. .___. |
| x 1 x x 2 x | 3 | x | 5
| .___.___. x . . .___. x .___. . |
| | 2 x 2 | 2 | 1 x | 2 x | 4
| . x . x . x . . x . x .___.___.___. |
| | 1 x | | x x x | | 3
| . x . .___. x .___. x .___.___.___. |
| | x | 3 | 2 | 2 x | 2
| . x .___.___. x . . x .___.___.___. |
| | 3 | x 2 | 3 | 2 | 2 x 2 x 3 | | 1
| .___. x . x .___. x .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
We are close to the end. The last two steps will not be shown (they
can be figured out easily). Solving the puzzle does not take much time.
The writing of each step takes time, but it is as important as the writing
(taking a written record) of a chess game by the chess players.
Afterwards we can double-check for errors, review the whole solution
(looking for improvements, like avoiding unnecessary steps),
draw conclusions (new patterns appeared ?), etc.
For instance, after completing the solution of this puzzle,
it is natural to ask if the solution path would be much longer
without that uniqueness step. If the answer to that is yes,
it gives more value to the uniqueness move!
I propose the following Slitherlink tough puzzle
to be solved manually.
(From Simon Tatham's Portable Puzzle Collection)

Initial configuration in text format (and notation)
.-------------------------------------------.
| . . . . . . . . . . . |
| 1 3 2 | 10
| . . . . . . . . . . . |
| 3 0 2 1 2 1 | 9
| . . . . . . . . . . . |
| 3 1 3 | 8
| . . . . . . . . . . . |
| 1 3 1 3 | 7
| . . . . . . . . . . . |
| 3 3 2 | 6
| . . . . . . . . . . . |
| 3 1 2 1 | 5
| . . . . . . . . . . . |
| 2 0 3 3 3 | 4
| . . . . . . . . . . . |
| 2 2 2 2 0 | 3
| . . . . . . . . . . . |
| 2 2 1 3 | 2
| . . . . . . . . . . . |
| 2 3 2 | 1
| . . . . . . . . . . . |
'-------------------------------------------'
a b c d e f g h i j
Recalling Notation:
(3r)c6 means to place a line segment at the right-edge
of cell c6 (has a number 3 on it); ( b)a1 means to place
a line segment at the bottom of the cell a1, which has
no number in it; (2xr)b3 means to place an 'x' at the
right-edge of cell b3, which has number 2 in it.
Rules:
1. Connect adjacent dots with vertical or horizontal lines to make a single loop.
2. The numbers indicate how many lines surround it, while empty cells may be surrounded by any number of lines.
3. The loop never crosses itself and never branches off.
Update 1 (April 14, 2025)
In this puzzle one can go far before getting stuck due to
many easy patterns available. The following configuration
is obtained after a sequence of forced moves
STEP 1
.-------------------------------------------.
| . .___. x . x .___.___.___. x .___.___. |
| | | x 1 | 3 | | 2 | | 10
| .___. x .___. x .___. .___. x . x . . |
| | 3 x 0 x 2 | 1 x | | x 2 | 1 x | | 8
| .___. x . x . x . . . .___. x .___. |
| 3 | 1 x | x | 3 | 8
| .___. x . x .___. . . . . x .___. |
| | x 1 x 3 1 3 | | 7
| .___. x .___. . . . . . .___. |
| 3 | | 3 2 x | | x | 6
| .___. x . . . . .___. x .___. x . |
| | 3 x 1 | x 2 | x 1 x x | 5
| .___. . . . x .___. x .___. .___. |
| 2 x 0 x 3 | x | 3 | 3 | | 4
| . . . . . x .___. x . x .___. . |
| 2 2 2 2 | x x 0 x x | | 3
| . . . . . . . x . x . . . |
| 2 2 1 x 3 | 2
| . . . . . . . . . . . |
| 2 3 2 | 1
| . . . . . . . . . . . |
'-------------------------------------------'
a b c d e f g h i j
The path for (3)j2 can be continued easily
due to an immediate contradiction if one considers
(3r)j2 true. So, Step 1 for me ends at
.-------------------------------------------.
| . .___. . .___.___.___. .___.___. |
| | | 1 | 3 | | 2 | | 10
| .___. .___. .___. .___. . . . |
| | 3 0 2 | 1 | | x 2 | 1 | | 8
| .___. . . x . . . .___. .___. |
| 3 | 1 | x | 3 | 8
| .___. . .___. . . . . x .___. |
| | 1 x 3 1 3 | | 7
| .___. .___. . . . . . .___. |
| 3 | | 3 2 x | | | 6
| .___. x . . . . .___. .___. . |
| | 3 x 1 | x 2 | 1 | 5
| .___. . . . x .___. x .___. .___. |
| 2 x 0 x 3 | x | 3 | 3 | | 4
| . . . . . x .___. x . x .___. . |
| 2 2 2 2 | x x 0 x | | 3
| . . . . . . . x . x . .___. |
| 2 2 1 x | 3 | 2
| . . . . . . . .___. .___. |
| 2 3 | 2 | | 1
| . . . . . . . . .___.___. |
'-------------------------------------------'
a b c d e f g h i j
What to do next ?
Update 2 (Apr 15, 2025)
Step 2: One can prove quickly that (1b)g2 is false.
(I did not check if this is the best option)
So, (1l)g2 is true, and further progress can be made:
.-------------------------------------------.
| . .___. . .___.___.___. .___.___. |
| | | 1 | 3 | | 2 | | 10
| .___. .___. x .___. .___. . . . |
| | 3 0 2 | 1 x | | x 2 | 1 | | 9
| .___. . . x . . x . .___. .___. |
| x 3 | 1 | x | 3 | 8
| .___. . .___. x . . . . x .___. |
| | 1 x | 3 1 x 3 | | 7
| .___. .___. . . . . . .___. |
| 3 | | 3 2 | x | | | 6
| .___. x . . . . X .___. x .___. . |
| | 3 x 1 | x 2 | x 1 x | 5
| .___. . . . x .___. x .___. x .___. |
| x 2 x 0 x 3 | x | 3 | 3 | | 4
| . . . .___. x .___. x . x .___. . |
| 2 2 x 2 | 2 | x x 0 x | | 3
| . . . . x . x .___. x . x . .___. |
| 2 | x 2 | 1 x | 3 | 2
| . . . . x .___. x . x .___. .___. |
| 2 3 | | | | 2 | | 1
| . . . .___.___. x .___. x .___.___. |
'-------------------------------------------'
a b c d e f g h i j
Again: What to do next ?
Final Update (Apr 17, 2024)
Step 3: to prove that (3r)f7 is false.
After that, the puzzle is nearly solved:
.-------------------------------------------.
| . .___. . .___.___.___. .___.___. |
| | | 1 | 3 | | 2 | | 10
| .___. .___. .___. .___. . . . |
| | 3 0 2 | 1 | | 2 | 1 | | 9
| .___. . . .___. .___.___. .___. |
| 3 | 1 | | | 3 | 8
| .___. . .___. .___.___.___. .___. |
| | 1 | 3 1 | 3 | | 7
| .___. .___.___. .___. . . .___. |
| 3 | | 3 | 2 | | | | 6
| .___. x .___. .___. .___. .___. . |
| | 3 x 1 x | x | 2 | 1 | 5
| .___.___. . x . x .___. .___. .___. |
| x 2 x 0 x 3 | | 3 | 3 | | 4
| . . . .___. x .___. . .___. . |
| 2 2 x 2 | 2 | 0 | | 3
| . . . . x . .___. . . .___. |
| 2 | 2 | 1 | 3 | 2
| . . . . x .___. . .___. .___. |
| 2 3 | | | | 2 | | 1
| . . . .___.___. .___. .___.___. |
'-------------------------------------------'
a b c d e f g h i j
We cannot have ( b)c5 because that would create an undesirable loop.
So, ( r)b4 is forced, and this allows one to finish the puzzle in a
few elementary moves.
The final configuration is
.-------------------------------------------.
| . .___. . .___.___.___. .___.___. |
| | | 1 | 3 | | 2 | |
| .___. .___. .___. .___. . . . |
| | 3 0 2 | 1 | | 2 | 1 | |
| .___. . . .___. .___.___. .___. |
| 3 | 1 | | | 3 |
| .___. . .___. .___.___.___. .___. |
| | 1 | 3 1 | 3 | |
| .___. .___.___. .___. . . .___. |
| 3 | | 3 | 2 | | | |
| .___. .___. .___. .___. .___. . |
| | 3 1 | | 2 | 1 |
| .___.___. . . .___. .___. .___. |
| 2 | | 0 3 | | 3 | 3 | |
| .___.___. .___. .___. . .___. . |
| | 2 2 2 | 2 | 0 | |
| . .___.___. . .___. . . .___. |
| | | 2 | | 2 | 1 | 3 |
| . . .___. .___. . .___. .___. |
| | | 2 | 3 | | | | 2 | |
| .___. .___.___.___. .___. .___.___. |
'-------------------------------------------'
The next puzzle of this kind will be a lot harder !
I propose the following Slitherlink tough puzzle
to be solved manually (this one is my creation).
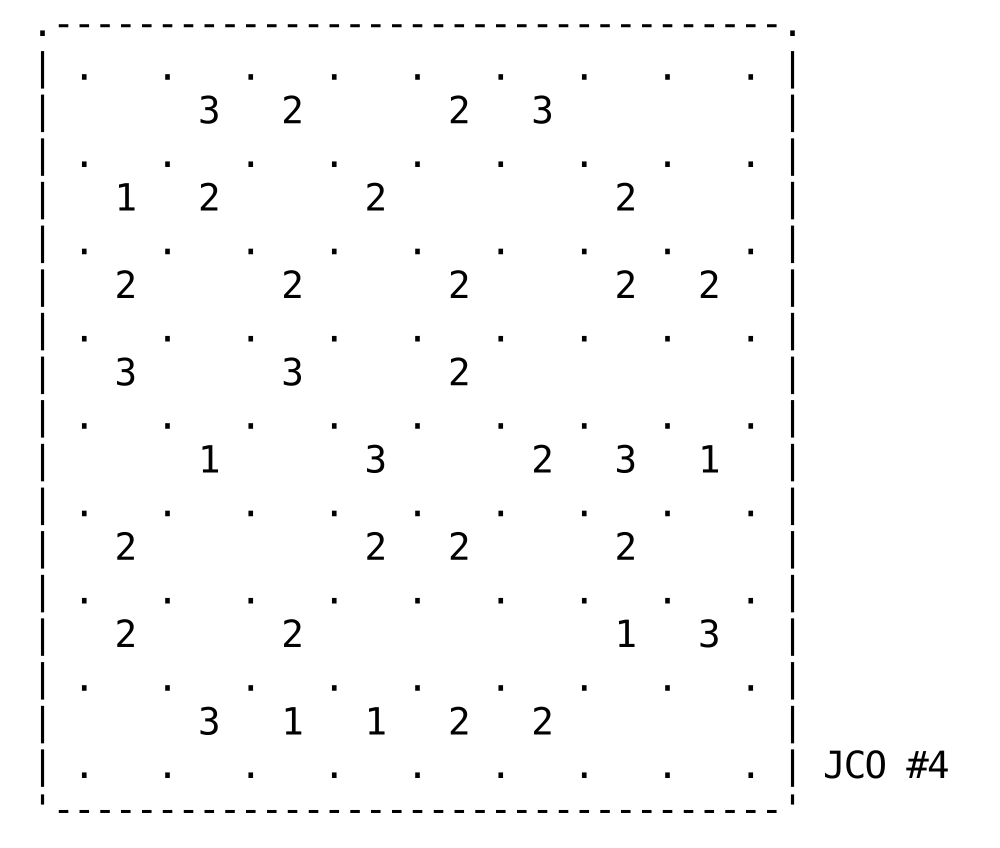
Initial configuration in text format
.-----------------------------------.
| . . . . . . . . . |
| 3 2 2 3 | 8
| . . . . . . . . . |
| 1 2 2 2 | 7
| . . . . . . . . . |
| 2 2 2 2 2 | 6
| . . . . . . . . . |
| 3 3 2 | 5
| . . . . . . . . . |
| 1 3 2 3 1 | 4
| . . . . . . . . . |
| 2 2 2 2 | 3
| . . . . . . . . . |
| 2 2 1 3 | 2
| . . . . . . . . . |
| 3 1 1 2 2 | 1
| . . . . . . . . . |
'-----------------------------------'
a b c d e f g h JCO#4
Step 1: basic moves
.-----------------------------------.
| . . . .___. . . . . |
| | 3 2 2 3 | 8
| . . . . . . . . . |
| 1 2 2 2 | 7
| . . . . . . . . . |
| 2 x 2 2 2 2 | 6
| . . x .___. . . . . . |
| | 3 | 3 2 | 5
| . . . . . . . . . |
| 1 3 | 2 3 1 | 4
| . . . .___. . . . . |
| 2 2 2 | 2 | 3
| . . . . .___. x . . . |
| 2 2 x 1 3 | 2
| . . . . . . . . . |
| 3 1 1 2 2 | 1
| . . . . . . . . . |
'-----------------------------------'
a b c d e f g h JCO #4
. pattern 3-3 in diagonal, that also implies (2r)e3, (2b)e3
. pattern 2-2-2 in diagonal close to a corner: (3l)a5, ( t)d8
. (3l)b8 must be true (immediate)
How to continue ?
Update (Apr 21, 2025)
For sure there are many ways to
solve this puzzle after that start.
I divided my solution path into 5 steps.
The second step has 3 easy deductions (not shown):
. (3r)b1 must be true
. (3t)h2 must ge true
. (3t)b1 must be false (so (2l)a3 is true)
So, my step 2 ends with the configuration
.-----------------------------------.
| . . . .___. . . . . |
| | 3 2 2 3 | 8
| . x . . . . . . . . |
| 1 2 2 2 | 7
| . . . . . . . . . |
| 2 2 2 2 2 | 6
| . . .___. . . . . . |
| | 3 | 3 2 | 5
| . . . . . . . . . |
| 1 3 | 2 3 1 | 4
| . . . .___. x . . . . |
| | 2 2 x 2 | 2 | 3
| . . . . .___. x . .___. |
| 2 | 2 x 1 3 | 2
| . . x . x . . . . . . |
| x | 3 | 1 x 1 2 2 | 1
| . x .___. x . x . . . . . |
'-----------------------------------'
a b c d e f g h JCO #4
How to proceed ?
Update (April 22, 2025)
Step 3 is the main part: to show that (1t)d1 can't be true.
Assuming the contrary, we reach the following
.-----------------------------------.
| . . . .___. . . . . |
| | 3 2 2 3 | 8
| . x . . . . . . . . |
| 1 2 2 2 | 7
| . . . . . . . . . |
| 2 2 2 2 2 | 6
| . . .___. . . . . . |
| | 3 | 3 2 | 5
| . . . . . . . . . |
| 1 3 | 2 3 1 | 4
| . . . .___. x . . . . |
| | 2 2 x 2 | 2 | 3
| . . . x . .___. x . .___. |
| 2 | 2 | x x 1 3 | 2
| . . x . x ._?_.___. x . x .___. |
| x | 3 | 1 x 1 x 2 | 2 x | 1
| . x .___. x . x . x .___.___. . |
'-----------------------------------'
a b c d e f g h JCO #4
Now I considered the possible configurations for (3)h2:
both lead to contradiction, and so (1t)d1 is false.
That gives
.-----------------------------------.
| . . . .___. x .___. . . |
| | 3 2 | 2 | 3 | 8
| . x . . . . x . . . . |
| 1 2 2 2 | 7
| . . . . . . . . . |
| 2 2 2 x 2 2 x | 6
| . . .___. .___. x . .___. |
| | 3 | 3 x 2 | x x | | 5
| . . . .___. x . x .___.___. |
| 1 3 | | 2 | 3 x 1 x | 4
| . . . x .___. x . x .___. x . |
| | 2 x | 2 x 2 | x 2 | x | 3
| . . x .___. x .___. x . x .___. |
| 2 | 2 x | x x 1 x 3 | | 2
| . . x . x . x . x . x .___.___. |
| x | 3 | 1 x 1 | 2 x 2 | | 1
| . x .___. x . x .___.___. . . |
'-----------------------------------'
a b c d e f g h JCO #4
This ends step 3.
How to proceed ?
Final update (April 23, 2025)
We can't have ( l)a4 true (quick contradiction at (2t)a6), so
(2t)a3 is true and we can reach
.-----------------------------------.
| . .___. .___. .___. . . |
| | 3 | 2 | | 2 | 3 | 8
| . . . . . x . . . . |
| 1 | 2 | | 2 | 2 | 7
| . . .___. .___. . . . |
| 2 | 2 2 x 2 2 x | 6
| .___. .___.___.___. x . .___. |
| | 3 | 3 2 | x x | | 5
| .___. .___.___. . .___.___. |
| | 1 3 | | 2 | 3 1 | 4
| .___. . .___. . .___. . |
| | 2 | 2 2 | 2 | | 3
| . . .___. .___. . .___. |
| | 2 | 2 | 1 3 | | 2
| .___. . . . . .___.___. |
| | 3 | 1 1 | 2 2 | | 1
| . .___. . .___.___. . . |
'-----------------------------------'
a b c d e f g h JCO #4
Now, the end is simple (not shown).
The final configuration is
.-----------------------------------.
| . .___. .___. .___. . . |
| | 3 | 2 | | 2 | 3 | | 8
| . . . . . . . . . |
| 1 | 2 | | 2 | | | 2 | 7
| . . .___. .___. .___. . |
| 2 | 2 2 2 | 2 | 6
| .___. .___.___.___. . .___. |
| | 3 | 3 2 | | | 5
| .___. .___.___. . .___.___. |
| | 1 3 | | 2 | 3 1 | 4
| .___. . .___. . .___. . |
| | 2 | 2 2 | 2 | | 3
| . . .___. .___. . .___. |
| | 2 | 2 | 1 3 | | 2
| .___. . . . . .___.___. |
| | 3 | 1 1 | 2 2 | | 1
| . .___. . .___.___. . . |
'-----------------------------------'
a b c d e f g h JCO #4
I propose the following interesting Slitherlink puzzle.
(puzzle from Simon Tatham's Collection)
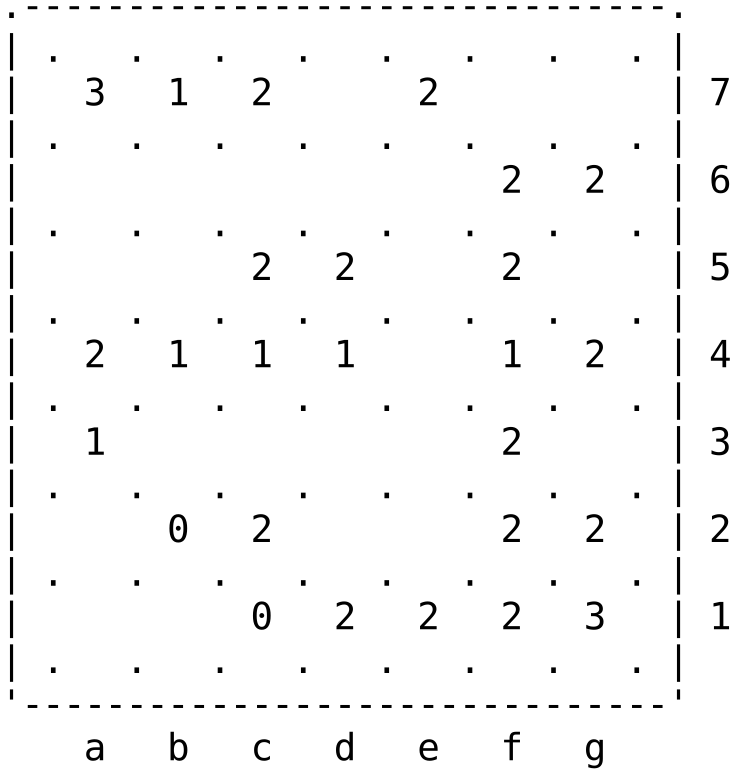
.-------------------------------.
| . . . . . . . . |
| 3 1 2 2 | 7
| . . . . . . . . |
| 2 2 | 6
| . . . . . . . . |
| 2 2 2 | 5
| . . . . . . . . |
| 2 1 1 1 1 2 | 4
| . . . . . . . . |
| 1 2 | 3
| . . . . . . . . |
| 0 2 2 2 | 2
| . . . . . . . . |
| 0 2 2 2 3 | 1
| . . . . . . . . |
'-------------------------------'
a b c d e f g
Rules:
1. Connect adjacent dots with vertical or horizontal lines to make a single loop.
2. The numbers indicate how many lines surround it, while empty cells may be surrounded by any number of lines.
3. The loop never crosses itself and never branches off.
Update (Aug 18, 2025)
The following moves come without effort
.-------------------------------.
| .___. . . . . . . |
| | 3 1 x 2 2 | 7
| . . x . . . . . . |
| 2 2 | 6
| . . . . . . . . |
| 2 2 2 | 5
| . . . . . . . . |
| 2 1 1 1 1 2 | | 4
| . . . . . . . . |
| 1 | 2 | | | 3
| . . .___. . . .___. |
| 0 2 | | 2 2 | 2
| . . . .___. .___.___. |
| 0 2 | 2 2 3 | | 1
| . . . . .___.___.___. |
'-------------------------------'
a b c d e f g
Looking at (1)a3, there is only one place that avoids
being stuck at the lower left corner: (1t)a3. That gives
(2l)a4, ( l)a5, (0t)b2
.-------------------------------.
| .___. . . . . . . |
| | 3 1 x 2 2 | 7
| . . x . . . . . . |
| 2 2 | 6
| . . . . . . . . |
| | 2 2 2 | 5
| . . . . . . . . |
| | 2 1 1 1 1 2 | | 4
| .___.___. . . . . . |
| 1 | 2 | | | 3
| . . .___. . . .___. |
| 0 2 | | 2 2 | 2
| . . . .___. .___.___. |
| 0 2 | 2 2 3 | | 1
| . . . . .___.___.___. |
'-------------------------------'
a b c d e f g
How to continue ?
Update (Aug 20, 2025)
From (1b)c4, we see that we must have
(2b)c5, (2l)c5 and so (2b)d5
.-------------------------------.
| .___. . . . . . . |
| | 3 1 x 2 2 | 7
| . . x . . . . . . |
| 2 2 | 6
| . . . x . . . . . |
| | | 2 x 2 2 | 5
| . . x .___.___. . x . . |
| | 2 x 1 x 1 x 1 x x 1 2 | | 4
| .___.___. x . x . . . . |
| 1 | 2 | | | 3
| . . .___. . . .___. |
| 0 2 | | 2 2 | 2
| . . . .___. .___.___. |
| 0 2 | 2 2 3 | | 1
| . . . . .___.___.___. |
'-------------------------------'
a b c d e f g
Now the only way for (2l)f2 to proceed
is to turn left, up, right and meet (2r)f3,
otherwise, i.e., (2l)f3, forces ( b)e4 and
that line has to place to go. So,
.-------------------------------.
| .___. . . . . . . |
| | 3 1 x 2 2 | 7
| . . x . . . . . . |
| 2 2 | 6
| . . . x . . . . . |
| | | 2 x 2 2 | | 5
| . x . x .___.___. . x .___. |
| | 2 1 x 1 x 1 x x 1 2 | | 4
| .___.___. x . .___.___. . |
| 1 | x | 2 | | | 3
| . . .___. .___. x .___. |
| 0 2 | | 2 2 | 2
| . . . .___. .___.___. |
| 0 2 | 2 2 3 | | 1
| . . . . .___.___.___. |
'-------------------------------'
a b c d e f g
How to continue ?
Update (Aug 20, 2025)
Now, (1l)b7 is not possible because it leads to
a quick contradiction at (2)c7, so (1t) b7!,
(2t)c7, (3b)a7, ( r)a6, ( b)a6, ( l)c6, (2b)c7,
( t)d7
.-------------------------------.
| .___.___.___.___. . . . |
| | 3 1 2 2 | 7
| .___. .___. . . . . |
| | | 2 2 | 6
| .___. . . . . . . |
| | | 2 2 2 | | 5
| . . .___.___. . x .___. |
| | 2 1 1 1 x x 1 2 | | 4
| .___.___. . .___.___. . |
| 1 | | 2 | | | 3
| . . .___. .___. x .___. |
| 0 2 | | 2 2 | 2
| . . . .___. .___.___. |
| 0 2 | 2 2 3 | | 1
| . . . . .___.___.___. |
'-------------------------------'
a b c d e f g
We are close to the finishing the puzzle.
How to continue ?
Update (Aug 21, 2025)
One key observation now is that we
cannot have (2b)g6 [it means a line at
the bottom of cell (2)g6], because we get
an immediate contradiction at cell (2)e7:
--------------.
___. . . . |
2 x | 7
. x .___. . |
| 2 x 2 | 6
. . x ._?_. |
2 | | 5
. . . . |
So x at (2b)g6, and x at (2r)g6,
so (2l)g6, (2t)g6, ( r)g7, ( t)g7,
(2l)f6
.-------------------------------.
| .___.___.___.___. . .___. |
| | 3 1 2 2 | | 7
| .___. .___. . . .___. |
| | | | 2 | 2 x | 6
| .___. . . . . . x . |
| | | 2 2 2 | | 5
| . . .___.___. . x .___. |
| | 2 1 1 1 x x 1 2 | | 4
| .___.___. . .___.___. . |
| 1 | | 2 | | | 3
| . . .___. .___. x .___. |
| 0 2 | | 2 2 | 2
| . . . .___. .___.___. |
| 0 2 | 2 2 3 | | 1
| . . . . .___.___.___. |
'-------------------------------'
a b c d e f g
and the rest is easy.
.-------------------------------.
| .___.___.___.___. .___.___. |
| | 3 1 2 | 2 | | | 7
| .___. .___. . . .___. |
| | | | | | 2 | 2 | 6
| .___. . .___. . . . |
| | | 2 2 | 2 | | 5
| . . .___.___.___. .___. |
| | 2 1 1 1 1 2 | | 4
| .___.___. . .___.___. . |
| 1 | | 2 | | | 3
| . . .___. .___. .___. |
| 0 2 | | 2 2 | 2
| . . . .___. .___.___. |
| 0 2 | 2 2 3 | | 1
| . . . . .___.___.___. |
'-------------------------------'
a b c d e f g
This Slitherlink puzzle is a bit harder!
(puzzle from Simon Tatham's Collection)
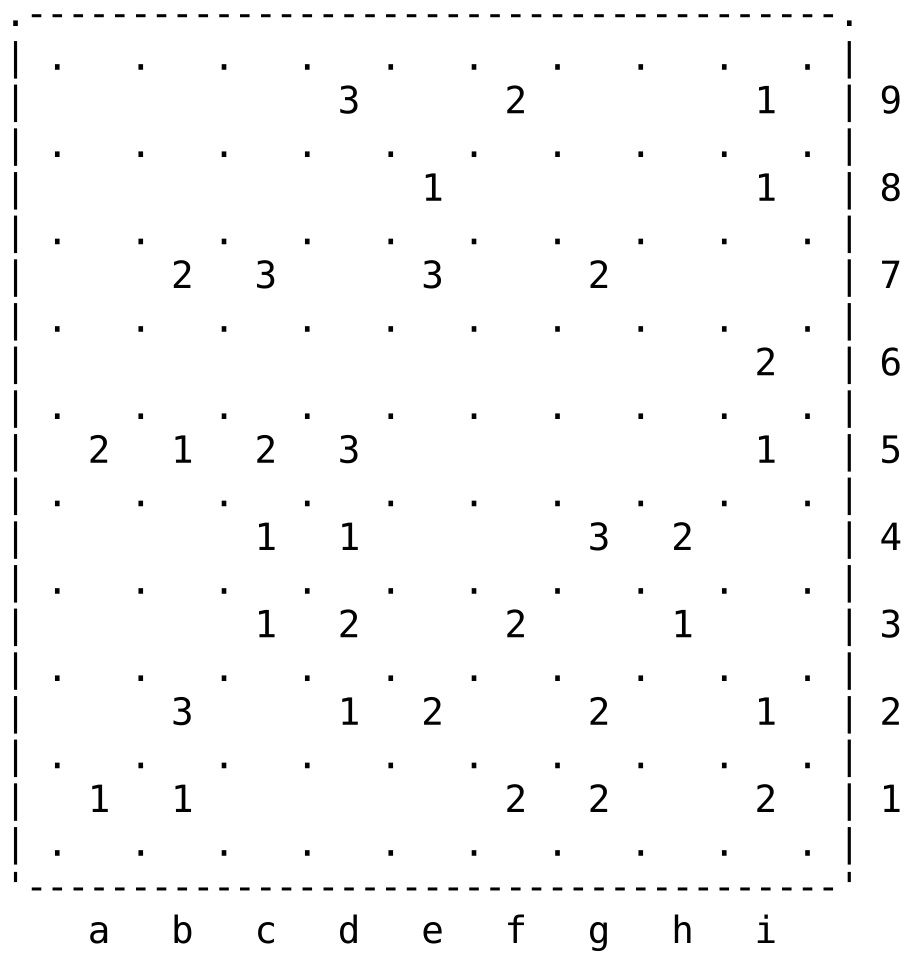
.---------------------------------------.
| . . . . . . . . . . |
| 3 2 1 | 9
| . . . . . . . . . . |
| 1 1 | 8
| . . . . . . . . . . |
| 2 3 3 2 | 7
| . . . . . . . . . . |
| 2 | 6
| . . . . . . . . . . |
| 2 1 2 3 1 | 5
| . . . . . . . . . . |
| 1 1 3 2 | 4
| . . . . . . . . . . |
| 1 2 2 1 | 3
| . . . . . . . . . . |
| 3 1 2 2 1 | 2
| . . . . . . . . . . |
| 1 1 2 2 2 | 1
| . . . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
Update (Aug 18, 2025)
A good start is 1.(1l)i9 [only viable possibility],
2.( t)h9 followed by 3.( t)h9.
Something similar happens at (1)a1:
4.(1t)a1, 5.( l)a2, 6.( l)a3, and 7.(3t)b2, 8.(3r)b2
Next, inspect the corner (2)i1. It only makes sense to
link the lower left corner of that cell to the top right corner,
and due to (1)i2, there is only one way 9.(2b)i1, 10.(2r)i1.
Then, 11.( r)i3 and 12.( b)h1 follow.
.---------------------------------------.
| . . . . . . . .___. x . |
| 3 2 | 1 x | 9
| . . . . . . . . . x . |
| 1 1 x | 8
| . . . . . . . . . . |
| 2 3 3 2 | 7
| . . . . . . . . . . |
| 2 | 6
| . . . . . . . . . . |
| 2 1 2 3 1 | 5
| . . . . . . . . . . |
| 1 1 3 2 | 4
| . . . . . . . . . . |
| x 1 2 2 1 | | 3
| . .___. x . . . . . . x . |
| | 3 | 1 2 2 x 1 | | 2
| .___. . . . . . . . . |
| x 1 x 1 2 2 2 | | 1
| . x . . . . . . .___.___. |
'---------------------------------------'
a b c d e f g h i
How to proceed ?
Update (Aug 20, 2025)
We notice that we cannot have a line at (1b)h3 or (1r)h3, and this
gives the pattern
. . . .____. .
3 3
. . . => . . .
1 x 1 x
. . x . . . x .
So, 13.(3t)g4, 14.(3l)g4
.---------------------------------------.
| . . . . . . . .___. x . |
| 3 2 | 1 x | 9
| . . . . . . . . . x . |
| 1 1 x | 8
| . . . . . . . . . . |
| 2 3 3 2 | 7
| . . . . . . . . . . |
| 2 | 6
| . . . . . . . . . . |
| 2 1 2 3 1 | 5
| . . . . . . .___. . . |
| 1 1 | 3 2 | 4
| . . . . . . . . . . |
| x 1 2 2 1 x | | 3
| . .___. x . . . . . x . x . |
| | 3 | 1 2 2 x 1 | | 2
| .___. . . . . . . . . |
| x 1 x 1 2 2 2 | | 1
| . x . . . . . . .___.___. |
'---------------------------------------'
a b c d e f g h i
This is the important moment. How to proceed ?
(it is odd: we are already close to solving this puzzle!)
Update (Aug 22, 2025)
. (1t)c3 is false [i.e., we can't have a line at the top of (1)c3],
because to the right it has to continue at (2t)d3, so no line
is possible at (1t)d4 and (1t)c4 and we must have (3l)d5,(3t)d5,(3r)d5 and
the line at (3l)d5 has no place to go (down).
.---------------------------------------.
| . . . . . . . .___. x . |
| 3 2 | 1 x | 9
| . . . . . . . . . x . |
| 1 1 x | 8
| . . . . . . . . . . |
| 2 3 3 2 | 7
| . . . . . . . . . . |
| 2 | 6
| . . . .___. . . . . . |
| 2 1 2 | 3 | 1 | 5
| . . . x ? x . . .___. . . |
| 1 1 | 3 2 | 4
| . . .___.___. . . . . . |
| x 1 2 2 1 x | | 3
| . .___. x . . . . . x . x . |
| | 3 | 1 2 2 x 1 | | 2
| .___. . . . . . . . . |
| x 1 x 1 2 2 2 | | 1
| . x . . . . . . .___.___. |
'---------------------------------------'
a b c d e f g h i
So, 15.(2l)d3 !
Now, (x) at (1t)d5 and at (1r)d4
gives 16.(3l)d5, 17.(3t)d5, 18.(3r)d5,
19.( b)e5
.---------------------------------------.
| . . . . . . . .___. x . |
| 3 2 | 1 x | 9
| . . . . . . . . . x . |
| 1 1 x | 8
| . . . . . . . . . . |
| 2 3 3 2 | 7
| . . . . . . . . . . |
| x x 2 | 6
| . . . x .___. x . . . . . |
| 2 1 2 | 3 | x x 1 | 5
| . . . . x .___. x .___. x . . |
| x 1 1 x | 3 2 | 4
| . . . x . . . . . . . |
| | x 1 | 2 2 1 x | | 3
| . .___. x . . . . . x . x . |
| | 3 | 1 x 2 2 x 1 | | 2
| .___. . . x . . . . . . |
| x 1 x 1 2 2 2 | | 1
| . x . . . . . . .___.___. |
'---------------------------------------'
a b c d e f g h i
The unlocking is near. How to finish the puzzle ?
Update (Aug 24, 2025)
Now, 20.(3r)g4! (otherwise contradiction at (2)e2),
and 21.(2r)e2! (only way coming from the line (3l)g4,
due to (x) at (2l)e2)
.---------------------------------------.
| . . . . . . . .___. x . |
| 3 2 | 1 x | 9
| . . . . . . . . . x . |
| 1 1 x | 8
| . . . . . . . . . . |
| 2 3 3 2 | 7
| . . . . . . . . . . |
| x x 2 | 6
| . . . x .___. x . . . . . |
| 2 1 2 | 3 | x 1 | 5
| . . . . x .___. x .___. . . |
| 1 1 x | 3 | 2 | 4
| . . . x . . . . . . . |
| | x 1 | 2 2 1 x | | 3
| . .___. x . . . . . x . x . |
| | 3 | 1 x 2 | 2 x 1 | | 2
| .___. . . x . . . . . x . |
| x 1 x 1 2 2 2 | | 1
| . x . x . . . . . .___.___. |
'---------------------------------------'
a b c d e f g h i
Now 22.(2b)e2, 23.( r)d1,
.---------------------------------------.
| . . . . . . . .___. x . |
| 3 2 | 1 x | 9
| . . . . . . . . . x . |
| 1 1 x | 8
| . . . . . . . . . . |
| 2 3 3 2 | 7
| . . . . . . . . . . |
| x x 2 | 6
| . . . x .___. x . . . . . |
| 2 1 2 | 3 | x 1 | 5
| . . . . x .___. x .___. . . |
| 1 1 x | 3 | 2 | 4
| . . . x . . . . . . . |
| | x 1 | 2 2 1 x | | 3
| . .___. x . . . . . x . x . |
| | 3 | 1 x 2 | 2 x 1 | | 2
| .___. . . x .___. . . . x . |
| x 1 x 1 | 2 2 2 | | 1
| . x . x . . . . . .___.___. |
'---------------------------------------'
a b c d e f g h i
and the continuation is easy, starting, for
instance, at (2)f1: 24. (2r)f1, 25.(2b)f1,
26. ( b)e1, 27.(2r)g1, 28.(2r)g2, 29.(2l)g2,
30.( l)g3, 31.(1l)h3, 32.(2r)h4, 33.( t)i3 etc
.---------------------------------------.
| . . . . . . . .___. x . |
| 3 2 | 1 x | 9
| . . . . . . . . . x . |
| 1 1 x | 8
| . . . . . . . .___.___. |
| 2 3 3 2 | | 7
| . . . . . . . . .___. |
| x x | 2 x | 6
| . . . x .___. x . . . . x . |
| 2 1 2 | 3 | x | 1 x | 5
| . . . . x .___. x .___. . . |
| 1 1 x | 3 | 2 | | 4
| . . . x . . . . . .___. |
| | x 1 | 2 2 | | 1 x | | 3
| . .___. x . . . . . x . x . |
| | 3 | 1 x 2 | | 2 | x 1 | | 2
| .___. . . x .___. . . . x . |
| x 1 x 1 | 2 | 2 | 2 | | 1
| . x . x . . .___.___. .___.___. |
'---------------------------------------'
a b c d e f g h i
We have many moves ahead, but no obstacle.
The final configuration is
.---------------------------------------.
| .___.___.___. .___.___.___.___. . |
| | | 3 | 2 | 1 | 9
| . .___. .___. .___. .___. . |
| | | | 1 | | | 1 | 8
| . . . .___. . . .___.___. |
| | | 2 | 3 | | 3 | | 2 | | 7
| . . .___. .___. .___. .___. |
| | | | | 2 | 6
| .___. . .___. .___.___. . . |
| 2 1 2 | 3 | | | 1 | 5
| .___.___.___. .___. .___. . . |
| | 1 1 | 3 | 2 | | 4
| . . . .___.___. . . .___. |
| | 1 | 2 | 2 | | 1 | | 3
| . .___. . . . . . . . |
| | | 3 | | 1 2 | | 2 | 1 | | 2
| .___. . . .___. . . . . |
| 1 1 | | | 2 | 2 | 2 | | 1
| . . .___. .___.___. .___.___. |
'---------------------------------------'
a b c d e f g h i
I propose this interesting (many patterns) and harder Slitherlink puzzle.
(puzzle from Simon Tatham's Collection)
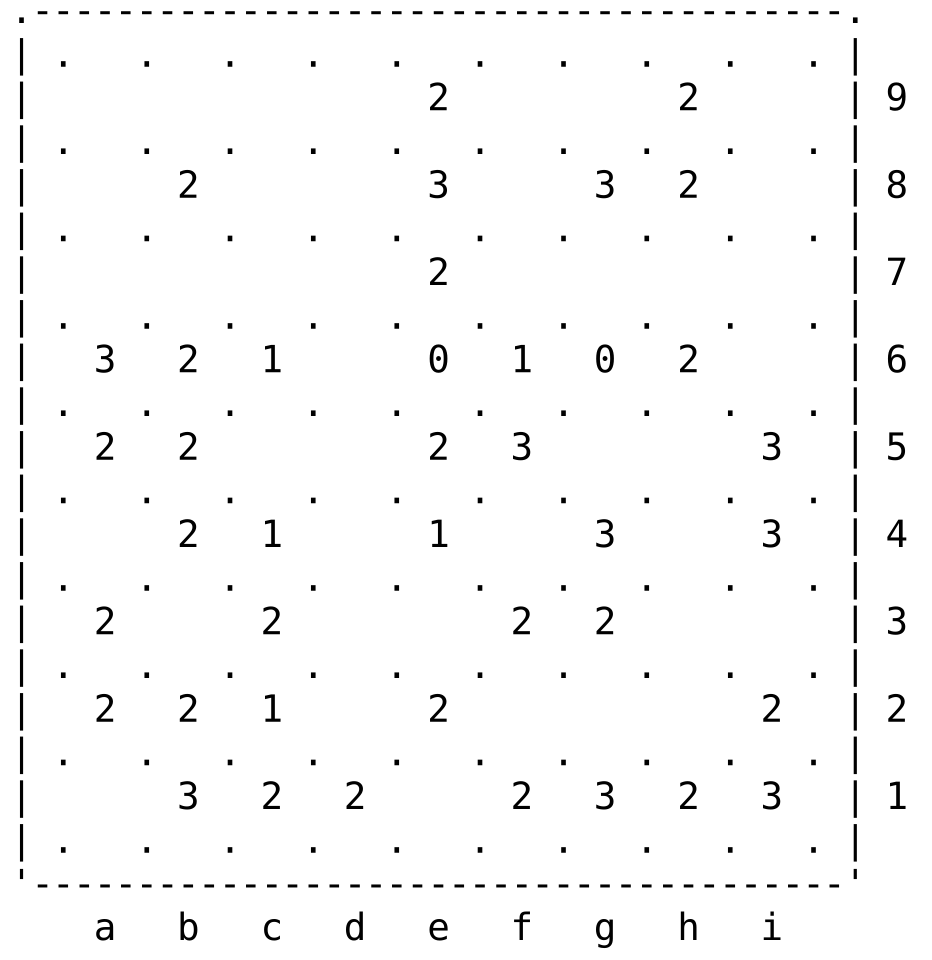
.---------------------------------------.
| . . . . . . . . . . |
| 2 2 | 9
| . . . . . . . . . . |
| 2 3 3 2 | 8
| . . . . . . . . . . |
| 2 | 7
| . . . . . . . . . . |
| 3 2 1 0 1 0 2 | 6
| . . . . . . . . . . |
| 2 2 2 3 3 | 5
| . . . . . . . . . . |
| 2 1 1 3 3 | 4
| . . . . . . . . . . |
| 2 2 2 2 | 3
| . . . . . . . . . . |
| 2 2 1 2 2 | 2
| . . . . . . . . . . |
| 3 2 2 2 3 2 3 | 1
| . . . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
Update (Aug 25, 2025)
Step 1: Basic moves
1.(3r)i1, 2.(3b)i1, 3.(3t)i5, 4.(3b)i5
5.(3b)i4, 6.( l)a4, 7.(2b)d1, 8.(3t)f5,
9.(3l)f5, 10.(3r)f5, 11.(2l)e7, 12.(2t)e7,
13.(3r)e8, 14.(3t)e8, 15.( b)d7, 16.(3l)g8,
17.(3b)g8, 18.(3r)g4, 19.(3b)g4
.---------------------------------------.
| . . . . . . . . . . |
| 2 x 2 | 9
| . . . . .___. x . . . . |
| 2 3 | | 3 2 | 8
| . . . . x .___. x .___. . . |
| | 2 x x | 7
| . . . .___. x . x . x . . . |
| 3 2 1 x 0 x 1 x 0 x 2 | 6
| . . . . . x .___. x . .___. |
| 2 2 2 | 3 | 3 | 5
| . . . . . . . . x .___. |
| | 2 1 x 1 3 | 3 | 4
| . . . . . x . .___. x .___. |
| 2 2 2 2 x | 3
| . . . . . . . . . . |
| 2 2 1 2 2 | 2
| . . . . . . . . . . |
| 3 2 2 2 3 2 3 | | 1
| . . . .___. . . . .___. |
'---------------------------------------'
a b c d e f g h i
How to make progress from here ?
Update (Aug 26, 2025)
Step 2: In any configuration involving cell
(2)e9, we must have 20.( t)d9! Also,
we cannot have (3l)i5 because of (2)h6, so
21.(3r)i5!, 22.(3l)i4, 23.( r)g7!, 24.(2r)h8,
25.(2t)h8
.---------------------------------------.
| . . . .___. . . . . . |
| 2 x 2 x | 9
| . . . . .___. x . .___. x . |
| 2 3 | | 3 x 2 | | 8
| . . . . x .___. x .___. x . . |
| | 2 x x | | 7
| . . . .___. x . x . x . . . |
| 3 2 1 x 0 x 1 x 0 x 2 x | 6
| . . . . . x .___. x . .___. |
| 2 2 2 | 3 | 3 | | 5
| . . . . . . . . x .___. |
| | 2 1 x 1 3 | | 3 x | 4
| . . . . . x . .___. x .___. |
| 2 2 2 2 x x | 3
| . . . . . . . . . . |
| 2 2 1 2 2 | 2
| . . . . . . . . . . |
| 3 2 2 2 3 2 3 | | 1
| . . . .___. . . . .___. |
'---------------------------------------'
a b c d e f g h i
and a lot more moves are available up to
move 39. What would be the configuration
after that move ?
Update (Aug 27, 2025)
After 39 moves, we reach the following
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 2 2 | | 9
| . . . .___.___. .___.___. . |
| 2 3 | | 3 2 | | | 8
| . . . . x .___. .___. .___. |
| | 2 | | 7
| . . . .___. . . .___. . |
| 3 2 1 x 0 1 0 2 | | 6
| . . . . . x .___. . .___. |
| 2 2 2 | 3 | 3 | | 5
| . . . . . . .___. .___. |
| | 2 1 x 1 3 | | 3 | 4
| . . . . . x . .___. .___. |
| 2 2 2 2 x x | | 3
| . . . . . . . . . . |
| 2 2 1 2 2 | 2
| . . . . . . . . . . |
| 3 2 2 2 3 2 3 | | 1
| . . . .___. . . . .___. |
'---------------------------------------'
a b c d e f g h i
How to proceed ?
(we need several deductions to unlock this puzzle!)
Update (Aug 28, 2025)
This is the key position for this puzzle! It requires careful analysis
to find a good way to make progress. The procedure is to manually check
(i.e., explore) different alternatives until something promising appears.
Step 3: For this puzzle, a powerful way is to see the consequences of (2l)a5.
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 2 2 | | 9
| . . . .___.___. .___.___. . |
| 2 3 | | 3 2 | | | 8
| . . . . x .___. .___. .___. |
| | 2 | | 7
| . . . .___. . . .___. . |
| 3 2 1 x 0 1 0 2 | | 6
| . . . . . x .___. . .___. |
|?| 2 2 2 | 3 | 3 | | 5
| . . . . . . .___. .___. |
| | 2 1 x 1 3 | | 3 | 4
| . . . . . x . .___. .___. |
| 2 2 2 2 x x | | 3
| . . . . . . . . . . |
| 2 2 1 2 2 | 2
| . . . . . . . . . . |
| 3 2 2 2 3 2 3 | | 1
| . . . .___. . . . .___. |
'---------------------------------------'
a b c d e f g h i
Now there are two ways for the cell (3)a6.
Both lead to contradictions (how ?)
So,
55.(2b)a5!! 56.(3l)a6 57.(3b)a6 58.(2b)b4
59.(2t)b4
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 2 2 | | 9
| . . . .___.___. .___.___. . |
| 2 3 | | 3 2 | | | 8
| . . . . .___. .___. .___. |
| | 2 | | 7
| . . . .___. . . .___. . |
| | 3 2 1 x 0 1 0 2 | | 6
| .___. . . . x .___. . .___. |
| 2 2 2 | 3 | 3 | | 5
| .___.___. . . . .___. .___. |
| | 2 x 1 x 1 3 | | 3 | 4
| .___.___. . . x . .___. .___. |
| 2 2 2 2 | | 3
| .___.___. . . . . .___. . |
| | 2 2 1 2 | 2 | | 2
| . .___. . . . . . . . |
| | | 3 | 2 2 2 3 | 2 | 3 | | 1
| .___. .___.___. . .___. .___. |
'---------------------------------------'
a b c d e f g h i
How to continue ?
Update (Aug 30, 2025)
Step 4: 60.(1t)c2 is not possible, since it
leads quickly to trouble at cell (2)f1
[please verify this]. So,
60.(1r)c2!! 61.(2t)d1 62.(2l)c3 63.(2r)c3
64.( b)e1
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 2 2 | | 9
| . . . .___.___. .___.___. . |
| 2 3 | | 3 2 | | | 8
| . . . . x .___. .___. .___. |
| | 2 | | 7
| . . . .___. . . .___. . |
| | 3 2 1 x 0 1 0 2 | | 6
| .___. . . . x .___. . .___. |
| 2 x 2 2 | 3 | 3 | | 5
| .___.___. . . . .___. .___. |
| | 2 x 1 x 1 3 | | 3 | 4
| .___.___. x . . x . .___. .___. |
| 2 | 2 | 2 2 x | | 3
| .___.___. . . . . .___. . |
| | 2 2 1 | 2 | 2 | | 2
| . .___. .___. . . . x . . |
| | | 3 | 2 2 x 2 3 | 2 | 3 | | 1
| .___. .___.___.___. .___. .___. |
'---------------------------------------'
a b c d e f g h i
Now, it remains to find only one move to
unlock this tough puzzle.
Update (Aug 31, 2025)
One way to finish the puzzle is to see that
(2b)f1 leads quickly to problems at (2)f3:
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 2 2 | | 9
| . . . .___.___. .___.___. . |
| 2 3 | | 3 2 | | | 8
| . . . . x .___. .___. .___. |
| | 2 | | 7
| . . . .___. . . .___. . |
| | 3 2 1 x 0 1 0 2 | | 6
| .___. . . . x .___. . .___. |
| 2 x 2 2 | 3 | 3 | | 5
| .___.___. . . . .___. .___. |
| | 2 x 1 x 1 | 3 | | 3 | 4
| .___.___. x . . x .?? .___. .___. |
| 2 | 2 | | 2 2 x | | 3
| .___.___. . . .?? .___.___. . |
| | 2 2 1 | 2 | 2 | | 2
| . .___. .___. .___.___. x . . |
| | | 3 | 2 2 x 2 3 | 2 | 3 | | 1
| .___. .___.___.___._?_.___. .___. |
'---------------------------------------'
a b c d e f g h i
So, 65.( r)e1!!
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 2 2 | | 9
| . . . .___.___. .___.___. . |
| 2 3 | | 3 2 | | | 8
| . . . . x .___. .___. .___. |
| | 2 | | 7
| . . . .___. . . .___. . |
| | 3 2 1 x 0 1 0 2 | | 6
| .___. . . . x .___. . .___. |
| 2 x 2 2 | 3 | 3 | | 5
| .___.___. . . . .___. .___. |
| | 2 x 1 x 1 3 | | 3 | 4
| .___.___. x . . x . .___. .___. |
| 2 | 2 | 2 2 x | | 3
| .___.___. . . . . .___. . |
| | 2 2 1 | 2 | 2 | | 2
| . .___. .___. . . . x . . |
| | | 3 | 2 2 x | 2 3 | 2 | 3 | | 1
| .___. .___.___.___. .___. .___. |
'---------------------------------------'
a b c d e f g h i
After this move the puzzle is unlocked with
no obstacles to its completion.
.---------------------------------------.
| .___.___.___.___.___.___.___.___.___. |
| | 2 2 | | 9
| . .___.___.___.___. .___.___. . |
| | | 2 3 | | 3 2 | | | 8
| .___. .___. .___. .___. .___. |
| | | | 2 | | 7
| .___.___. .___. . . .___. . |
| | 3 2 1 0 1 0 2 | | 6
| .___.___.___.___. .___. . .___. |
| 2 2 | 2 | 3 | 3 | | 5
| .___.___.___.___. . .___. .___. |
| | 2 1 1 | 3 | | 3 | 4
| .___.___. .___. . .___. .___. |
| 2 | 2 | | | 2 | 2 | | 3
| .___.___. . .___. . .___. . |
| | 2 2 1 | 2 | | | 2 | | 2
| . .___. .___.___. . . . . |
| | | 3 | 2 2 | 2 | 3 | 2 | 3 | | 1
| .___. .___.___.___. .___. .___. |
'---------------------------------------'
a b c d e f g h i
I propose this pleasant/smooth 9x9 Slitherlink puzzle.
(puzzle from Simon Tatham's Collection)
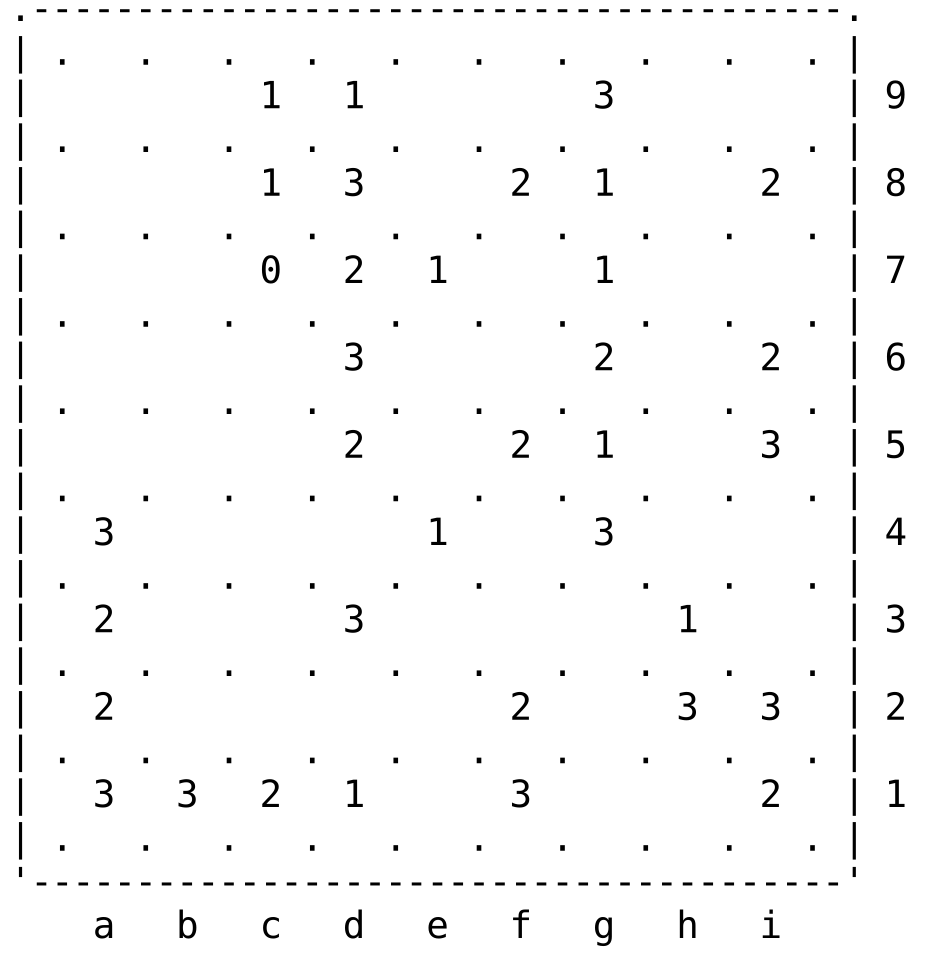
.---------------------------------------.
| . . . . . . . . . . |
| 1 1 3 | 9
| . . . . . . . . . . |
| 1 3 2 1 2 | 8
| . . . . . . . . . . |
| 0 2 1 1 | 7
| . . . . . . . . . . |
| 3 2 2 | 6
| . . . . . . . . . . |
| 2 2 1 3 | 5
| . . . . . . . . . . |
| 3 1 3 | 4
| . . . . . . . . . . |
| 2 3 1 | 3
| . . . . . . . . . . |
| 2 2 3 3 | 2
| . . . . . . . . . . |
| 3 3 2 1 3 2 | 1
| . . . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
Update (Sept 07, 2025)
Many basics moves available
.---------------------------------------.
| . . . . x . . . . . . |
| 1 1 x 3 | 9
| . . . x . . . . . . . |
| x 1 | 3 2 1 2 | 8
| . . . x .___. . . . . . |
| x 0 x 2 x 1 1 | 7
| . . . x .___. . . . . . |
| | 3 2 2 | 6
| . . . . . . . . . . |
| 2 2 1 3 | 5
| . . . . . . . . . . |
| | 3 1 3 | 4
| .___. . . . . . . . . |
| x 2 3 1 x | 3
| .___. . . . . . . .___. |
| | 2 x x 2 | 3 | 3 | | 2
| . .___. . x . . . .___. x . |
| | 3 | 3 | 2 x 1 x 3 x 2 | | 1
| .___. .___.___. . .___.___.___. |
'---------------------------------------'
a b c d e f g h i
Noticing that (1r)c9 is not possible, one can
advance with many moves in the top left part
of the puzzle and also in the top center.
Update (Sept 8, 2025)
.---------------------------------------.
| .___.___. . . . .___. . . |
| | | 1 1 | 3 | | 9
| . .___. .___.___.___. . . . |
| | | 1 | 3 2 1 2 | 8
| . . . .___.___.___. . . . |
| | | 0 2 1 1 x | 7
| . . . .___. . . x . . . |
| | | 3 | 2 2 | 6
| . . . . . . . . . . |
| 2 2 1 3 | 5
| . . . . . . . . . . |
| | 3 1 3 | 4
| .___. . . . . . . . . |
| 2 3 1 x x | 3
| .___.___. . . .___. . .___. |
| | 2 2 | 3 | 3 | | 2
| . .___. . . .___. .___. . |
| | 3 | 3 | 2 1 | 3 | 2 | | 1
| .___. .___.___.___. .___.___.___. |
'---------------------------------------'
a b c d e f g h i
How to continue ?
Update (Sept 10, 2025)
Now, looking at (3)g4, we cannot have
. .
3 |
.___.
because (1)h3 would be without possible lines.
So, for (3)g4, we must have
.___.
| 3
. .
and this has many implications (a few shown below)
.---------------------------------------.
| .___.___. . . . .___. . . |
| | | 1 1 | 3 | | 9
| . .___. .___.___.___. . . . |
| | | 1 | 3 2 1 2 | 8
| . . . .___.___.___. . . . |
| | | 0 2 1 1 x | 7
| . . . .___. . . x .___. . |
| | | 3 | | 2 | 2 | 6
| . . . . . .___. x .___. . |
| 2 | 2 x 1 x 3 | 5
| . . . . . . x .___. . . |
| | 3 x 1 | 3 | 4
| .___. . . . x . . . . . |
| 2 3 1 x x | 3
| .___.___. . . .___. . .___. |
| | 2 2 | 3 | 3 | | 2
| . .___. . . .___. .___. . |
| | 3 | 3 | 2 1 | 3 | 2 | | 1
| .___. .___.___.___. .___.___.___. |
'---------------------------------------'
a b c d e f g h i
Update (Sept 12, 2025)
.---------------------------------------.
| .___.___. . . . .___. .___. |
| | | 1 1 | 3 | | | | 9
| . .___. .___.___.___. . . . |
| | | 1 | 3 2 1 | | 2 | | 8
| . . . .___.___.___. .___. . |
| | | 0 2 1 | 1 | | 7
| . . . .___. . . .___.___. |
| | | 3 | | 2 | 2 | 6
| . . . . . .___. .___.___. |
| 2 | | 2 1 3 | | 5
| . . . . . . .___. .___. |
| | 3 1 | 3 | 4
| .___. . .___. . . . . . |
| 2 3 | 1 x x | 3
| .___.___. . . .___. . .___. |
| | 2 2 | 3 | 3 | | 2
| . .___. . . .___. .___. . |
| | 3 | 3 | 2 1 | 3 | 2 | | 1
| .___. .___.___.___. .___.___.___. |
'---------------------------------------'
a b c d e f g h i
Very close to solving. How to continue from here ?
Update (Sept 13, 2025)
We cannot have a vertical line to the left
of (1)h3, because the line on the top of (2)f2
would not have a place to go. So, (1t)h3, and
as a consequence
.---------------------------------------.
| .___.___. . . . .___. .___. |
| | | 1 1 | 3 | | | | 9
| . .___. .___.___.___. . . . |
| | | 1 | 3 2 1 | | 2 | | 8
| . . . .___.___.___. .___. . |
| | | 0 2 1 | 1 | | 7
| . . . .___. . . .___.___. |
| | | 3 | | 2 | 2 | 6
| . . . . . .___. .___.___. |
| 2 | | 2 1 3 | | 5
| . . . . . . .___. .___. |
| | 3 1 | 3 | | | 4
| .___. . .___. .___. .___. . |
| 2 3 | 1 | 3
| .___.___. . . .___.___. .___. |
| | 2 2 | 3 | 3 | | 2
| . .___. . . .___. .___. . |
| | 3 | 3 | 2 1 | 3 | 2 | | 1
| .___. .___.___.___. .___.___.___. |
'---------------------------------------'
a b c d e f g h i
Now there are three forced moves (with single
moves in between) that avoid loops and unlock
the puzzle. The first comes from the observation
that (1r)e4 would create a loop.
This gives 5 single moves to reach another easy
junction as this one. The puzzle is essentially
solved.
.---------------------------------------.
| .___.___. . . . .___. .___. |
| | | 1 1 | 3 | | | | 9
| . .___. .___.___.___. . . . |
| | | 1 | 3 2 1 | | 2 | | 8
| . . . .___.___.___. .___. . |
| | | 0 2 1 | 1 | | 7
| . .___. .___. . . .___.___. |
| | | | 3 | | 2 | 2 | 6
| .___. . . . .___. .___.___. |
| | | | 2 | | 2 1 3 | | 5
| .___. .___. .___. .___. .___. |
| | 3 1 | 3 | | | 4
| .___.___.___.___. .___. .___. . |
| 2 3 | | 1 | 3
| .___.___.___.___. .___.___. .___. |
| | 2 2 | 3 | 3 | | 2
| . .___. . . .___. .___. . |
| | 3 | 3 | 2 1 | 3 | 2 | | 1
| .___. .___.___.___. .___.___.___. |
'---------------------------------------'
a b c d e f g h i
I propose this 9x9 Slitherlink puzzle: full of patterns!
(this puzzle comes from Simon Tatham's Collection)
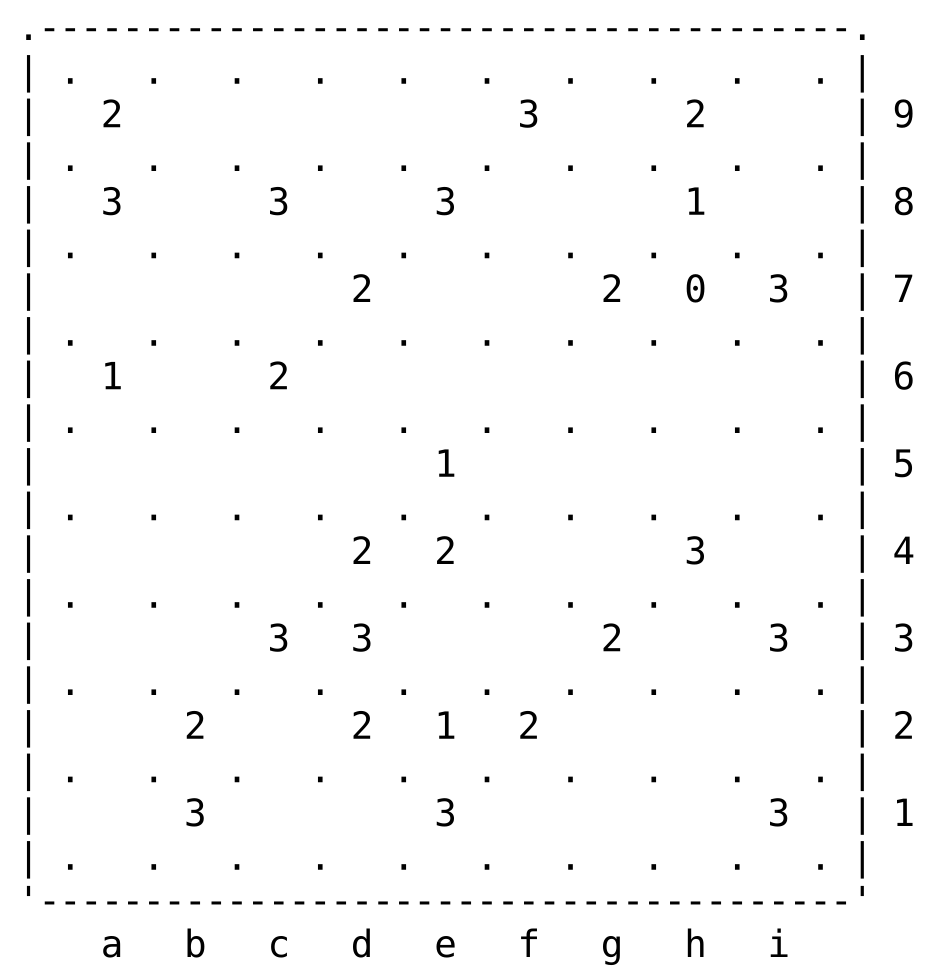
.---------------------------------------.
| . . . . . . . . . . |
| 2 3 2 | 9
| . . . . . . . . . . |
| 3 3 3 1 | 8
| . . . . . . . . . . |
| 2 2 0 3 | 7
| . . . . . . . . . . |
| 1 2 | 6
| . . . . . . . . . . |
| 1 | 5
| . . . . . . . . . . |
| 2 2 3 | 4
| . . . . . . . . . . |
| 3 3 2 3 | 3
| . . . . . . . . . . |
| 2 2 1 2 | 2
| . . . . . . . . . . |
| 3 3 3 | 1
| . . . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
Update (Oct 28, 2025)
Some simple patterns in this nice puzzle
_
3| _ .----------- . . . |
x 2 |3 | . .___. |
|3|3| 2 3| | 2 . . . |
x |3 -- | . . . 3 | |
-- | | . .___. |
| . . . -------------'
Update (Oct 29, 2025)
Without resistance, one can get the following position
.---------------------------------------.
| . .___.___. . .___. .___.___. |
| 2 | | | 3 | | 2 | | 9
| .___. .___. .___. .___. .___. |
| | 3 | 3 | 3 1 | | 8
| .___. .___. .___.___. . .___. |
| | | 2 x | 2 0 3 | | 7
| . x .___. .___. . .___. .___. |
| x 1 | 2 | | | | 6
| .___. x .___. .___.___.___. .___. |
| | | x | x 1 x | | 5
| . . . .___. .___. .___. . |
| | | x 2 | 2 | | | 3 | | | 4
| . . .___. . . . . . . |
| | | | 3 | 3 | | | 2 | | 3 | | 3
| . . . x .___. . . . .___. |
| | 2 x 2 1 | 2 | | | 2
| . . . .___. . . .___.___. |
| 3 | 3 | | 3 | | 1
| . . . . x .___. .___.___.___. |
'---------------------------------------'
a b c d e f g h i
and the end is easy.
I propose this interesting and hard Slitherlink puzzle.
(puzzle from Simon Tatham's Collection)

.-----------------------------------.
| . . . . . . . . . |
| 2 2 3 | 8
| . . . . . . . . . |
| 2 2 2 2 | 7
| . . . . . . . . . |
| 2 2 3 3 3 | 6
| . . . . . . . . . |
| 3 | 5
| . . . . . . . . . |
| 3 2 2 2 0 1 | 4
| . . . . . . . . . |
| 1 3 1 | 3
| . . . . . . . . . |
| 2 2 | 2
| . . . . . . . . . |
| 3 2 1 3 | 1
| . . . . . . . . . |
'-----------------------------------'
a b c d e f g h
Update (Nov 24, 2025)
We have many basic moves at the start.
Most of them are in the following grid
.-----------------------------------.
| . .___. . . .___.___.___. |
| 2 2 3 | | 8
| . . . . . . .___.___. |
| | 2 2 2 2 | 7
| . . . . . . . .___. |
| 2 2 3 3 3 | | 6
| . . . . . . . . . |
| |3 | 5
| . . . . . . .___. . |
| 3 2 2 2 0 1 | 4
| . . . . . .___. . . |
| 1 | 3 1 | 3
| . . . . . . . . . |
| 2 2 | 2
| . . . . . . . . . |
| | 3 2 1 3 | | 1
| .___. . . . . . .___. |
'-----------------------------------'
a b c d e f g h
Update (Nov 27, 2025)
. looking at (3)g3 to make progress at h1
. (2)f7 interacts with (3)e6
.-----------------------------------.
| . .___. . . .___.___.___. |
| 2 2 3 | | 8
| . . . . . . .___.___. |
| | 2 2 2 2 | 7
| . . . . . . . .___. |
| 2 2 3 | 3 3 | | 6
| . . . . x .___. . . . |
| x |3 | 5
| . . . . x . x . .___. . |
| 3 2 2 | 2 x 0 1 | 4
| . . . .___. x .___. . . |
| 1 | | 3 | 1 | 3
| . . . . . . .___. x . |
| 2 2 x | 2
| . . . . . . .___.___. |
| | 3 2 1 3 | | 1
| .___. . . . .___.___.___. |
'-----------------------------------'
a b c d e f g h
How to continue ?
Update (Nov 29, 2025)
Looking at (2)a2, the line at (3l)a1 must
enter (1)b3, so (x) at the top and right of
that cell. That makes impossible having a
line at (2)b4, so (2l)b4, (2t)b4, and (2t)c4,
etc
.-----------------------------------.
| . .___. . . .___.___.___. |
| 2 2 3 | | 8
| . . . . . . .___.___. |
| | 2 2 2 2 | 7
| . . . . . . . .___. |
| 2 2 3 | 3 3 | | 6
| . . . . .___. . . . |
| | |3 | 5
| . .___.___. . . .___. . |
| | 3 | 2 2 | 2 0 1 | 4
| .___. x . .___. .___. . . |
| 1 x | | 3 | 1 | 3
| . .___. . . . .___. x . |
| 2 2 x | 2
| . . . . . . .___.___. |
| | 3 2 1 3 | | 1
| .___. . . . .___.___.___. |
'-----------------------------------'
a b c d e f g h
How far can we go before getting stuck ?
It turns out a deduction is needed already!
.-----------------------------------.
| . .___. . . .___.___.___. |
| 2 2 3 | | 8
| . . . . . . .___.___. |
| | 2 2 2 2 | 7
| . . . . . . . .___. |
| 2 2 3 | 3 3 | | 6
| . . . . .___. . . . |
| | |3 | 5
| . .___.___. . . .___. . |
| | 3 | 2 2 | 2 0 1 | 4
| .___. x . .___. .___. . . |
| 1 x | | 3 | 1 | 3
| . .___. . . . .___. x . |
| 2 2 x | 2
| . . . . . . .___.___. |
| | 3 2 1 3 | | 1
| .___. . . . .___.___.___. |
'-----------------------------------'
a b c d e f g h
One possibility is to analyze where ( l)a5 should go.
( l)a6 is not possible because it quickly leads into
an impossible loop at cells b6,b7,c6.
So, (2b)a6 is forced and after many placements, we get
.-----------------------------------.
| .___.___.___. . .___.___.___. |
| | 2 | 2 | 3 | | 8
| . . . .___. . .___.___. |
| | 2 2 | | 2 | 2 | 7
| .___.___.___. . . . .___. |
| 2 2 3 | | 3 | 3 | | 6
| .___.___.___. .___. . . . |
| | |3 | 5
| . .___.___. . . .___. . |
| | 3 | 2 2 | 2 0 1 | 4
| .___. . .___. .___. . . |
| 1 | | 3 | 1 | 3
| . .___. . . . .___. . |
| 2 2 | 2
| . . . . . . .___.___. |
| | 3 2 1 3 | | 1
| .___. . . . .___.___.___. |
'-----------------------------------'
a b c d e f g h
What can we do next ?
Update (Nov 02, 2025)
(3r)g5 is not possible, because
it forces ( r)h5 to get an even number
of lines at row 5 and that leads to
trouble of a line at ( r)h4 that has
no place to go downwards. So, (3t)g5
is the only way, leading to
.-----------------------------------.
| .___.___.___. . .___.___.___. |
| | 2 | 2 | 3 | | 8
| . . . .___. . .___.___. |
| | 2 2 | | 2 | 2 | 7
| .___.___.___. . . .___.___. |
| 2 2 3 | | 3 | 3 | | 6
| .___.___.___. .___. .___.___. |
| | |3 | 5
| . .___.___. . . .___. . |
| | 3 | 2 2 | 2 0 1 | | 4
| .___. . .___. .___. . . |
| 1 | | | 3 | 1 | 3
| . .___. . . . .___. . |
| 2 2 | 2
| . . . . . .___.___.___. |
| | 3 2 1 3 | | 1
| .___. . . .___.___.___.___. |
'-----------------------------------'
a b c d e f g h
here we are very close to done.
Update (Nov 3, 2022)
Clearly the line ( r)e3 must go down to avoid a loop.
Also, (3t)a1 is not possible (why?) and the alternative
solves the puzzle with singles afterwards.
.-----------------------------------.
| .___.___.___. . .___.___.___. |
| | 2 | 2 | 3 | | 8
| . . . .___. . .___.___. |
| | 2 2 | | 2 | 2 | 7
| .___.___.___. . . .___.___. |
| 2 2 3 | | 3 | 3 | | 6
| .___.___.___. .___. .___.___. |
| | |3 | 5
| . .___.___. . . .___. . |
| | 3 | 2 2 | 2 0 1 | | 4
| .___. . .___. .___. . . |
| 1 | | | 3 | 1 | 3
| .___.___.___.___. . .___. . |
| | 2 2 | | 2
| . .___.___.___. .___.___.___. |
| | 3 | 2 1 | 3 | | 1
| .___. . . .___.___.___.___. |
'-----------------------------------'
a b c d e f g h
I have a more challenging Slitherlink puzzle (compared to SL# 16).
(puzzle from Simon Tatham's Collection)
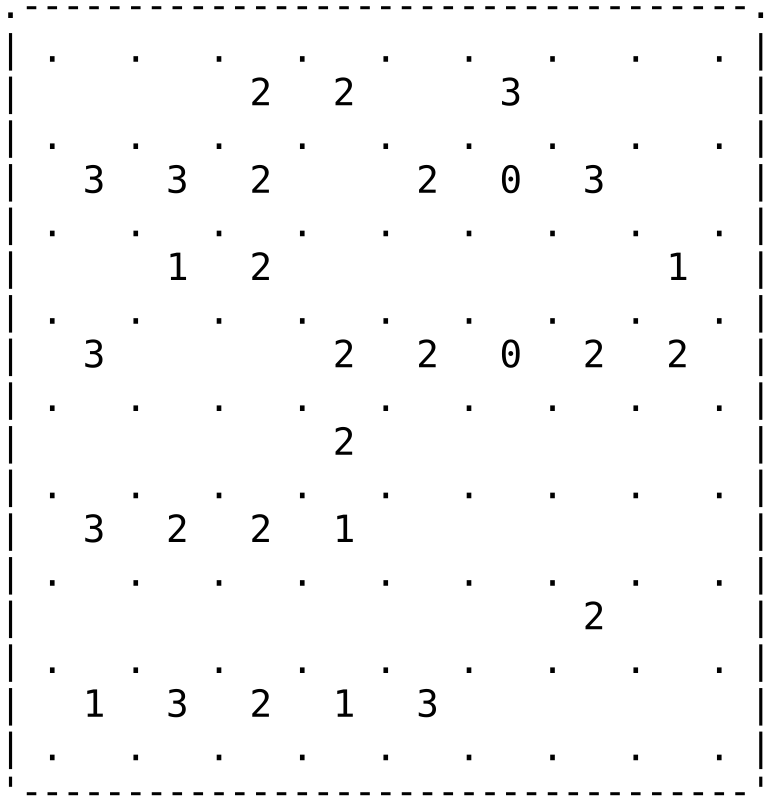
.-----------------------------------.
| . . . . . . . . . |
| 2 2 3 | 8
| . . . . . . . . . |
| 3 3 2 2 0 3 | 7
| . . . . . . . . . |
| 1 2 1 | 6
| . . . . . . . . . |
| 3 2 2 0 2 2 | 5
| . . . . . . . . . |
| 2 | 4
| . . . . . . . . . |
| 3 2 2 1 | 3
| . . . . . . . . . |
| 2 | 2
| . . . . . . . . . |
| 1 3 2 1 3 | 1
| . . . . . . . . . |
'-----------------------------------'
a b c d e f g h
Update (Dec4, 2025)
Basic moves
.-----------------------------------.
| . . . . . .___. . . |
| x 2 2 | 3 | | 8
| . . . . .___. .___. . |
| | 3 | 3 | 2 2 0 3 | | 7
| . . . . . . .___. x . |
| x 1 2 | x 1 | 6
| . . . . . . .___.___. |
| 3 2 2 0 x 2 x 2 | | 5
| . . . . . . .___. x . |
| 2 | | | | 4
| . . . . . . . . . |
| | 3 2 2 1 | 3
| .___. . . . . . . . |
| x 2 | 2
| . x . . . x . . . . . |
| x 1 | 3 2 x 1 3 | 1
| . x .___. . .___. . . . |
'-----------------------------------'
a b c d e f g h
Update (Dec 05, 2025)
Step 2: (2l)e7 is impossible because
creates a line at (2t)d8 without
place to go. So, (2b)e7 and a few
placements are available.
[recall notation: (2l)e7 means a line
in the left edge of the cell e7, that
has a 2 in it]
.-----------------------------------.
| . . . . . .___. . . |
| x 2 2 | 3 | | 8
| . . . . .___. .___. . |
| | 3 | 3 | 2 2 0 3 | | 7
| . . . .___.___. .___. . |
| x 1 2 | | 1 | 6
| . . . . .___. .___.___. |
| 3 2 2 0 2 2 | | 5
| . . . . . . .___. . |
| 2 | | | | 4
| . . . . . . . . . |
| | 3 2 2 1 | 3
| .___. . . . . . . . |
| 2 | 2
| . . . . x . . . . . |
| 1 | 3 2 x 1 3 | 1
| . .___. . .___. . . . |
'-----------------------------------'
a b c d e f g h
How to make progress from here ?
Update (Dec 7, 2025)
Step 3: Due to the line (2 t)e7, we must
have (2t)c8 ...
.-----------------------------------.
| . . .___. . .___. . . |
| x 2 2 | 3 | | 8
| . . . . .___. .___. . |
| | 3 | 3 | 2 2 0 3 | | 7
| . . . .___.___. .___. . |
| x 1 2 | | 1 | 6
| . . . . .___. .___.___. |
| 3 2 2 0 2 2 | | 5
| . . . . . . .___. . |
| 2 | | | | 4
| . . . . . . . . . |
| | 3 2 2 1 | 3
| .___. . . . . . . . |
| 2 | 2
| . . . . x . . . . . |
| 1 | 3 2 x 1 3 | 1
| . .___. . .___. . . . |
'-----------------------------------'
a b c d e f g h
and that line cannot go down: (2l)c8, (3b)b7
lead to impossibility at (2)c6, so ( t)b8 and
many placements follow:
.-----------------------------------.
| .___.___.___. . .___. . . |
| | 2 | 2 | 3 | | 8
| . .___. .___.___. .___. . |
| | 3 | 3 | 2 2 0 3 | | 7
| .___. .___.___.___. .___. . |
| 1 2 | | 1 | 6
| .___.___.___. .___. .___.___. |
| | 3 2 2 0 2 2 | | 5
| .___. . . . . .___. . |
| 2 | | | | 4
| .___. . . . . . . . |
| | 3 2 2 1 | 3
| .___. . . . . . . . |
| 2 | 2
| . . . . x . . . . . |
| 1 | 3 2 x 1 3 | 1
| . .___. . .___. . . . |
'-----------------------------------'
a b c d e f g h
Update (Dec 8, 2025)
Step 4: ( r)a2 is not possible because it
quickly leads to a loop.So (3t)b1
and many placemens follow.
.-----------------------------------.
| .___.___.___. . .___. . . |
| | 2 | 2 | 3 | | 8
| . .___. .___.___. .___. . |
| | 3 | 3 | 2 2 0 3 | | 7
| .___. .___.___.___. .___. . |
| 1 2 | | 1 | 6
| .___.___.___. .___. .___.___. |
| | 3 2 2 0 2 2 | | 5
| .___. . . . . .___. . |
| 2 | | | | 4
| .___. . . . . . . . |
| | 3 2 2 1 | 3
| .___.___. . . . . . . |
| | | 2 | 2
| . .___.___. x .___. . . . |
| 1 | 3 2 x 1 3 | | 1
| . .___.___.___.___. . . . |
'-----------------------------------'
a b c d e f g h
Now we need to resolve the center and that (2)g2 isolated
and this can be done in two more moves.
Update (Dec 9, 2025)
Step 5: ( r)a4 leads to an impossible situationat (2)d5.
[i.e., a line to the right of cell a4 leads to an impossibility]
So, (2t)b3! and many placements follow:
.-----------------------------------.
| .___.___.___. . .___. . . |
| | 2 | 2 | 3 | | 8
| . .___. .___.___. .___. . |
| | 3 | 3 | 2 2 0 3 | | 7
| .___. .___.___.___. .___. . |
| 1 2 | | 1 | 6
| .___.___.___.___.___. .___.___. |
| | 3 2 2 0 2 2 | | 5
| .___.___.___.___.___. .___. . |
| 2 | | | | | 4
| .___.___.___.___.___. . . . |
| | 3 2 2 1 | 3
| .___.___.___. .___.___. . . |
| | | 2 | 2
| . .___.___. .___. . . . |
| 1 | 3 2 1 3 | | 1
| . .___.___.___.___. . . . |
'-----------------------------------'
a b c d e f g h
The remaining is easy (4 lines in that
enclosed region).
I propose the following interesting Slitherlink puzzle.
(Source: Simon Tatham's Collection)
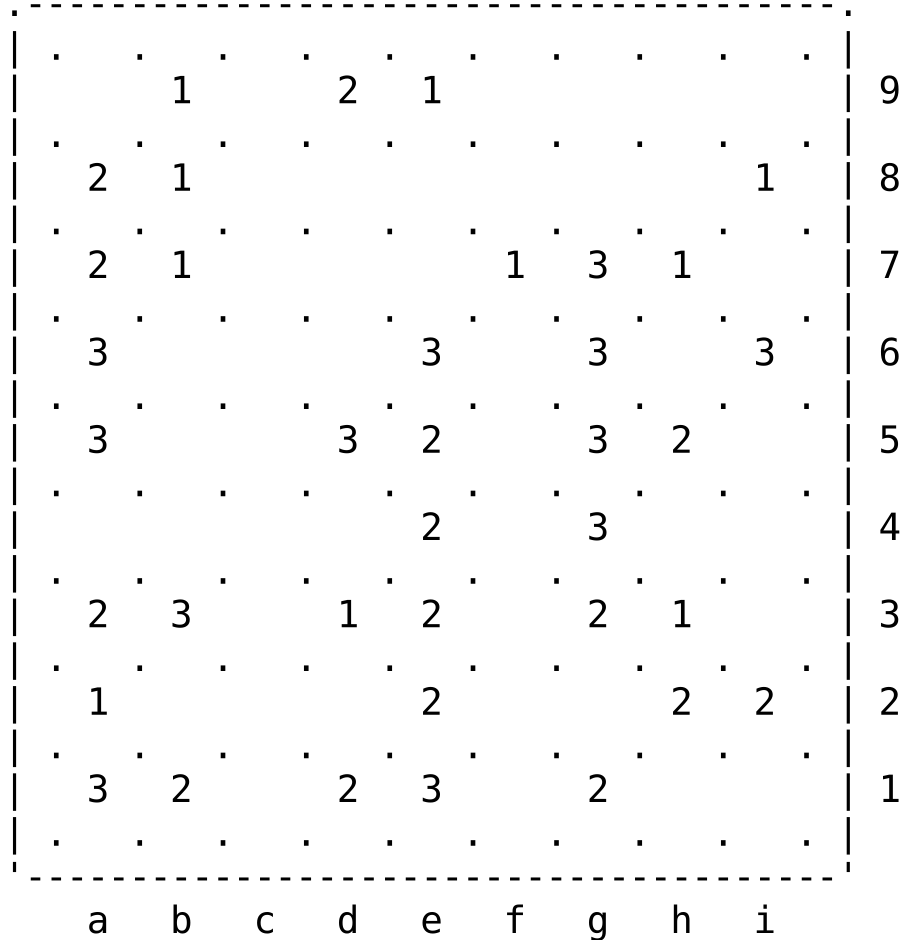
.---------------------------------------.
| . . . . . . . . . . |
| 1 2 1 | 9
| . . . . . . . . . . |
| 2 1 1 | 8
| . . . . . . . . . . |
| 2 1 1 3 1 | 7
| . . . . . . . . . . |
| 3 3 3 3 | 6
| . . . . . . . . . . |
| 3 3 2 3 2 | 5
| . . . . . . . . . . |
| 2 3 | 4
| . . . . . . . . . . |
| 2 3 1 2 2 1 | 3
| . . . . . . . . . . |
| 1 2 2 2 | 2
| . . . . . . . . . . |
| 3 2 2 3 2 | 1
| . . . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
Update (Jan 14, 2026)
In this puzzle, the start is very smooth !
The first 14 (very basic) of them are shown next
.---------------------------------------.
| . . . . . . . . . . |
| 1 2 1 | 9
| . . . . . . . . . . |
| 2 1 1 | 8
| . . . . . . . . . . |
| 2 1 1 3 1 | 7
| .___. . . .___. x .___. x . . |
| 3 3 | 3 3 | 6
| .___. x . . . . x .___. x . . |
| 3 | 3 2 3 2 | 5
| .___. . .___. . x .___. x . . |
| 2 3 | 4
| . . . . . . . . . . |
| 2 | 3 1 2 2 1 | 3
| . x .___. . . . . . . . |
| 1 x 2 2 2 | 2
| . . . . . . . . . . |
| | 3 2 2 3 2 | 1
| .___. . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
(One can continue without obstacles up to move 44)
Update (Jan 15, 2026)
After 44 moves we get
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 1 2 1 | | 9
| . . . . . .___.___.___.___. |
| 2 1 | 1 | 8
| . . . . . .___.___. . . |
| 2 1 1 3 | 1 | 7
| .___. . . .___. .___. .___. |
| 3 3 | | 3 | 3 | | 6
| .___. x . . . . .___. . . |
| 3 | 3 2 3 | 2 | | | 5
| .___. . .___. . x .___. . . |
| 2 | 3 | | | 4
| . . . . . . .___.___. . |
| 2 | 3 1 2 2 1 | | 3
| . X .___. . . . .___. . . |
| 1 x 2 | 2 2 | 2
| . . . . . . . . . . |
| | 3 2 2 3 2 | 1
| .___. . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
How to continue ?
Update (Jan 17, 2026)
We reached the first stop point.
Step 2: Looking at the right bottom corner of
the grid, the sequence (2r)i2, (2b)i2, (2b)h2
is impossible because it forces (2l)g1,(2b)g1,
and this line has not place to go at the
corner. Since (2r)i2, (2l)i2 is impossible,
we must have
45.(2t)i2! 46.(2l)i2 47.( l)i1 48.( b)h1
We get
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 1 2 1 | | 9
| . . . . . x .___.___.___.___. |
| 2 1 | 1 | 8
| . . . . . x .___.___. . . |
| 2 1 1 3 | 1 | 7
| .___. . . .___. .___. .___. |
| 3 3 | | 3 | 3 | | 6
| .___. x . . . . x .___. . . |
| 3 | 3 2 3 | 2 | | | 5
| .___. . .___. . x .___. . . |
| 2 | 3 | | | 4
| . . . . . . x .___.___. . |
| 2 | 3 1 2 2 1 | | 3
| . x .___. . . . .___. .___. |
| 1 x 2 | 2 | 2 | 2
| . . . . . . . . . . |
| | 3 2 2 3 2 | | 1
| .___. . . . . . .___. . |
'---------------------------------------'
How to make progress from here ?
Update (Jan 18, 2026)
(3l)a5 leads immediately to contradiction with (2)a3,
so 49.(3r)a5! 50.( l)a4 51.(3l)a6 and we reach:
.---------------------------------------.
| . . . .___.___.___.___.___.___. |
| 1 2 1 | | 9
| . . . . . x .___.___.___.___. |
| 2 1 | 1 | 8
| . . x . . . x .___.___. . . |
| x 2 1 x 1 3 | 1 | 7
| .___. . . .___. .___. .___. |
| | 3 x 3 | | 3 | 3 | | 6
| .___. x . . . . x .___. . . |
| 3 | | 3 2 3 | 2 | | | 5
| .___. . .___. . x .___. . . |
| | x 2 | 3 | | | 4
| . . . . . . x .___.___. . |
| 2 | 3 1 2 2 1 | | 3
| . x .___. . . . .___. .___. |
| 1 x 2 | 2 | 2 | 2
| . . . . . . . . . . |
| | 3 2 2 3 2 | | 1
| .___. . . . . . .___. . |
'---------------------------------------'
a b c d e f g h i
How to proceed from here ?
Update (Jan 19, 2026)
(2t)a8 leads to immediate contradiction, so
52.(2r)a7! and 11 more lines can ge placed.
We get the following configuration
.---------------------------------------.
| .___.___.___.___.___.___.___.___.___. |
| | 1 2 1 | | 9
| .___. . .___. .___.___.___.___. |
| 2 | 1 | | | 1 | 8
| . . . . . .___.___. . . |
| 2 | 1 | | 1 3 | 1 | 7
| .___. . . .___. .___. .___. |
| | 3 3 | | 3 | 3 | | 6
| .___. . . .___. x .___. . . |
| 3 | | 3 2 x 3 | 2 | | | 5
| .___. . .___. . x .___. . . |
| | x 2 | 3 | | | 4
| . . . . . . x .___.___. . |
| 2 | 3 1 2 2 1 | | 3
| . x .___. . . . .___. .___. |
| 1 x 2 | 2 | 2 | 2
| . . . . . . . . . . |
| | 3 2 2 3 2 | | 1
| .___. . . . . . .___. . |
'---------------------------------------'
a b c d e f g h i
How to continue from here ?
Update (Jan 20, 2026)
easy ending from here: for instance, (2)e5
cannot have non-parallel edges activated
(i.e., with lines on them) due to immediate
contradictions. So,
65.(2b)e5 66.(3t)d5 and 6 more lines lead to
.---------------------------------------.
| .___.___.___.___.___.___.___.___.___. |
| | 1 2 1 | | 9
| .___. . .___. .___.___.___.___. |
| 2 | 1 | | | 1 | 8
| . . . . . .___.___. . . |
| 2 | 1 | | 1 3 | 1 | 7
| .___. .___. .___. .___. .___. |
| | 3 | 3 | | 3 | 3 | | 6
| .___. . .___.___. .___. . . |
| 3 | | | 3 2 3 | 2 | | | 5
| .___. . .___.___. .___. . . |
| | x | 2 | | 3 | | | 4
| . . . . . . .___.___. . |
| 2 | 3 1 2 | 2 1 | | 3
| . x .___. . . . .___. .___. |
| 1 x 2 | 2 | 2 | 2
| . . . . . . . . . . |
| | 3 2 2 3 2 | | 1
| .___. . . . . . .___. . |
'---------------------------------------'
a b c d e f g h i
and the remaining offers very little resistance.
ADDED: The final configuration is
.---------------------------------------.
| .___.___.___.___.___.___.___.___.___. |
| | 1 2 1 | | 9
| .___. . .___. .___.___.___.___. |
| 2 | 1 | | | 1 | 8
| . . . . . .___.___. . . |
| 2 | 1 | | 1 3 | 1 | 7
| .___. .___. .___. .___. .___. |
| | 3 | 3 | | 3 | 3 | | 6
| .___. . .___.___. .___. . . |
| 3 | | | 3 2 3 | 2 | | | 5
| .___. . .___.___. .___. . . |
| | | 2 | | 3 | | | 4
| .___. . . . . .___.___. . |
| 2 | 3 | 1 2 | 2 1 | | 3
| . .___. .___.___. .___. .___. |
| 1 | 2 | | 2 | 2 | 2
| .___.___.___. .___. . . . . |
| | 3 2 2 | 3 | | 2 | | | 1
| .___.___.___.___. .___. .___. . |
'---------------------------------------'
a b c d e f g h i
The following Slitherlink puzzle is a lot harder than SL#18.
Interesting patterns that require thinking to take advantage of them.
(Source: Simon Tatham's Collection)
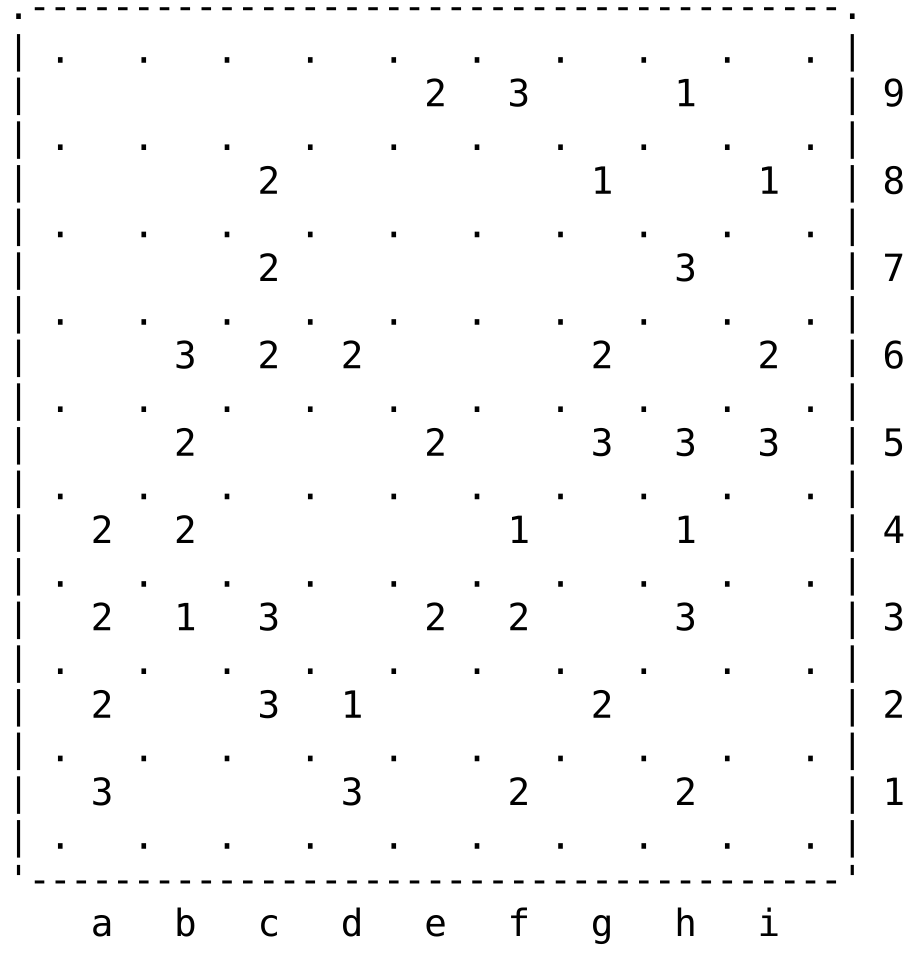
.---------------------------------------.
| . . . . . . . . . . |
| 2 3 1 | 9
| . . . . . . . . . . |
| 2 1 1 | 8
| . . . . . . . . . . |
| 2 3 | 7
| . . . . . . . . . . |
| 3 2 2 2 2 | 6
| . . . . . . . . . . |
| 2 2 3 3 3 | 5
| . . . . . . . . . . |
| 2 2 1 1 | 4
| . . . . . . . . . . |
| 2 1 3 2 2 3 | 3
| . . . . . . . . . . |
| 2 3 1 2 | 2
| . . . . . . . . . . |
| 3 3 2 2 | 1
| . . . . . . . . . . |
'---------------------------------------'
a b c d e f g h i
Update (Jan 16, 2026)
Step 1: 13 basic moves lead to
.---------------------------------------.
| . . . . . . . . . . |
| 2 3 1 | 9
| . . . . . . . . . . |
| 2 1 1 | 8
| . . . . . . . . . . |
| 2 3 | 7
| . . . . . . . . . . |
| 3 2 2 2 x x 2 | 6
| . . . . . . . . . . |
| 2 2 | 3 | 3 | 3 | | 5
| . . . . . . . . . . |
| 2 2 x 1 x 1 x | 4
| . . .___. x . . . . . . |
| 2 1 3 | 2 2 3 | 3
| . . x .___. x . . . . . . |
| 2 | 3 1 2 | 2
| . . x .___. . . . . . . |
| | 3 x 3 | 2 2 | 1
| .___. . .___. x . . . . . |
'---------------------------------------'
a b c d e f g h i
How to continue ?
Update (Jan 17, 2026)
Step 2:
We cannot have "x" at (3b)h3 [bottom of cell (3)h3]
because the line (3l)h2 [left edge of cell (3)h2] going
down to (2)f1 would meet that "x" at ( b)e1, having no
place to go. Same thing with "x" at (3l)h3. So,
14.(3b)h3! 15.(3l)h3! and 9 more placements using some
small deductions. We get
.---------------------------------------.
| . . . . . . . . . . |
| 2 3 1 x | 9
| . . . . . . . . . x . |
| 2 1 1 | 8
| . . . . . . . . . . |
| 2 3 | 7
| . . . . . . . . . . |
| 3 2 2 2 x x 2 | 6
| . . . . . . . . . . |
| | 2 2 | 3 | 3 | 3 | | 5
| . . . . . . . . . . |
| 2 2 | x 1 x 1 x | 4
| . . x .___. x . . . . . . |
| 2 | 1 3 | 2 2 | 3 | 3
| . . x .___. x . . . .___. . |
| 2 | 3 1 | | 2 | 2
| . . x .___. . . .___. . . |
| | 3 x 3 | | 2 2 | 1
| .___. . .___. x .___.___. . . |
'---------------------------------------'
a b c d e f g h i
How to make progress now ?
Update (Jan 18, 2026)
Step 3: (3b)g5 is not possible: it quickly
implies the existence of an impossible small loop.
So,
25.(3t)g5!! and 35 (!) placements can be made.
After all that, we reach the following configuration
.---------------------------------------.
| . . . .___. .___.___.___.___. |
| | 2 | 3 1 | | 9
| . . . . . .___. . . . |
| 2 | 1 1 | | 8
| . . . . .___.___. .___. . |
| 2 x | 3 | | | 7
| . . . . . .___.___. .___. |
| 3 2 2 2 2 | 6
| . . . . . . x .___. .___. |
| | 2 2 | 3 | 3 | 3 | | 5
| . . . . . .___. .___. . |
| 2 2 | x x 1 1 | | 4
| . . x .___. x .___. x .___. .___. |
| 2 | 1 3 | 2 | 2 | | 3 | | 3
| . . x .___. x . . . .___. . |
| 2 | 3 1 | | 2 | 2
| . . x .___. . . .___.___.___. |
| | 3 x 3 | | 2 2 | | 1
| .___. . .___. .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
For the next Step, how to advance from here ?
Update (Jan 19, 2026)
(1r)d2 [i.e., a line in the right edge of d2] would
lead to five lines at row 2 (impossible), so
61.(3t)d1!! and 19 more lines can be placed. We get
.---------------------------------------.
| . . . .___. .___.___.___.___. |
| | 2 | 3 1 | | 9
| . . . . . .___. . . . |
| 2 x | 1 1 | | 8
| . . .___. x .___.___. .___. . |
| | x 2 | | 3 | | | 7
| . .___. .___. .___.___. .___. |
| | | 3 | 2 x 2 2 2 | 6
| . . .___. . . x .___. .___. |
| | | 2 2 | | 3 | 3 | 3 | | 5
| . .___. . . x .___. .___. . |
| | 2 2 | x | 1 1 | | 4
| .___. .___. .___. .___. .___. |
| 2 | 1 3 | 2 | 2 | | 3 | | 3
| . . .___. . . . .___. . |
| 2 | | 3 1 | | 2 | 2
| .___. .___.___. . .___.___.___. |
| | 3 3 | | 2 2 | | 1
| .___.___.___.___. .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i
What would be a nice move 81 (that solves this
puzzle) ?
Update (Jan 21, 2026)
Looking at line 7, we have 5 lines. Since the
number of lines in any row/column must be even,
( r)d8 [a line at the right edge of cell d8]
must be false. So,
81.( r)d7!! and the remaining 13 moves are easy.
The final configuration is
.---------------------------------------.
| .___.___.___.___. .___.___.___.___. |
| | | 2 | 3 1 | | 9
| . .___.___.___. .___. . . . |
| | | 2 | 1 1 | | 8
| . .___.___. .___.___. .___. . |
| | 2 | | | 3 | | | 7
| . .___. .___. .___.___. .___. |
| | | 3 | 2 2 | 2 2 | 6
| . . .___.___. . .___. .___. |
| | | 2 | 2 | | 3 | 3 | 3 | | 5
| . .___. . . .___. .___. . |
| | 2 2 | | 1 1 | | 4
| .___. .___. .___. .___. .___. |
| 2 | 1 3 | 2 | 2 | | 3 | | 3
| . . .___. . . . .___. . |
| 2 | | 3 1 | | 2 | 2
| .___. .___.___. . .___.___.___. |
| | 3 3 | | 2 2 | | 1
| .___.___.___.___. .___.___.___.___. |
'---------------------------------------'
a b c d e f g h i